Question

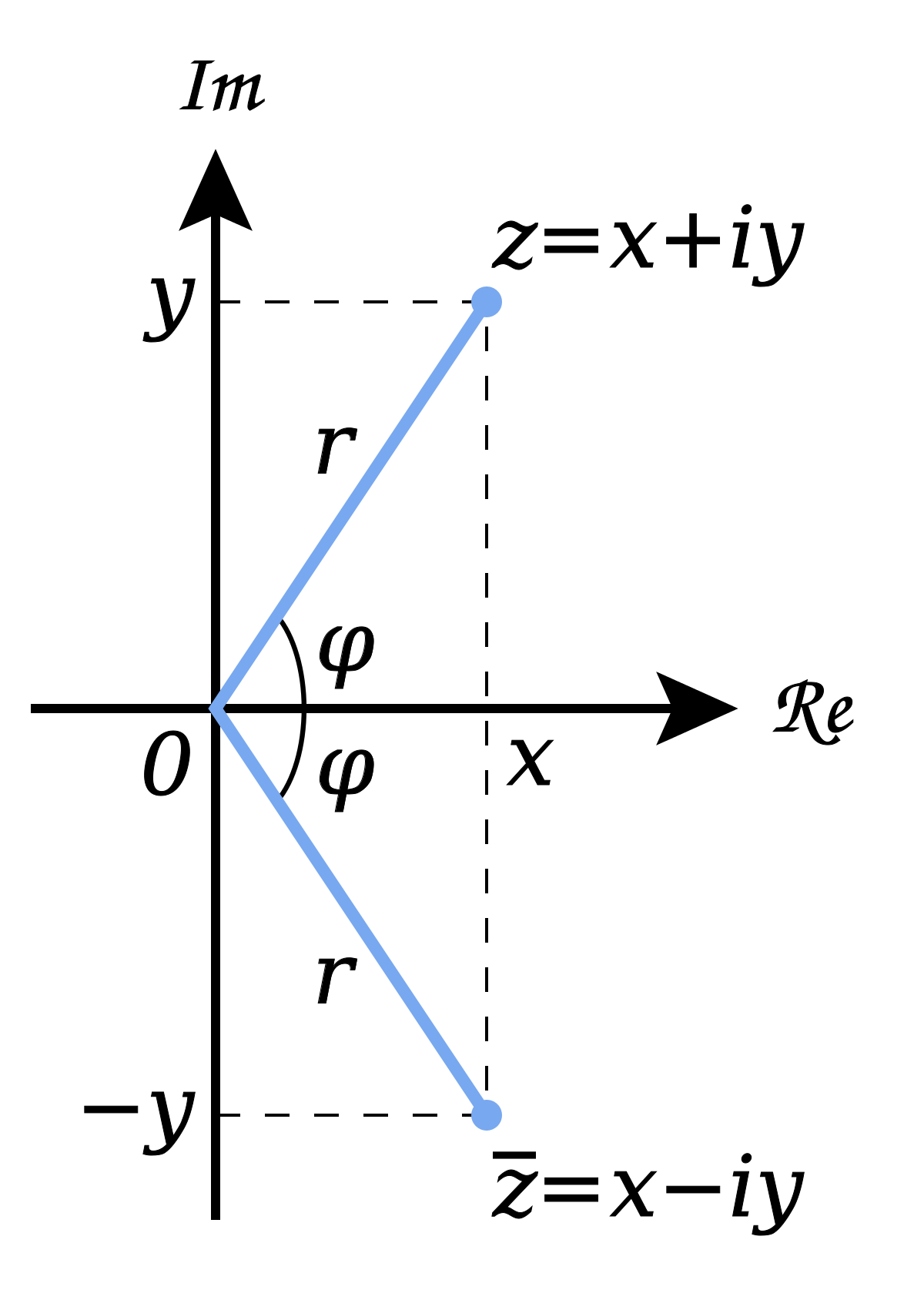
How do we represent complex numbers, their conjugate, modulus and argument of a complex numbers in argand plane?

Answer 1

Please see below.

Explanation:

Argand Plane is a plot of complex numbers as points on a two dimensional complex plane using `x`-axis as the real axis and `y`-axis as the imaginary axis.

In this plane every complex number, say `x+iy`, is represented by a point. Its reflection in real axis i.e. `x`-axis represents its conjugate complex number.

We can add two numbers by joining the two points representing the two numbers to `0+i0` (equivalent of origin) and then completing the parallelogram.

The length of line joining the number is its absolute value also known as modulus and the angle, this line makes with positive side of real axis or `x`-axis is known as argument of the number.

The number appears as: