Question #6b302
1 Answer
The length of the altitude
Explanation:
Your situation looks like this:
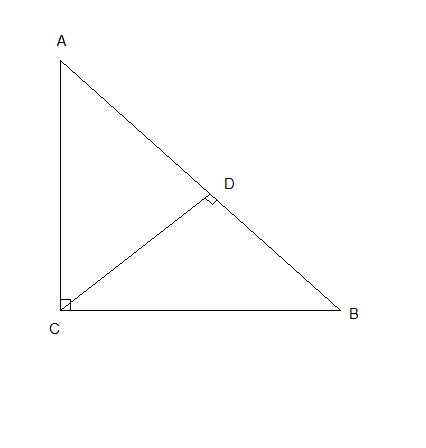
There is a right angle between AC and BC and a right angle between AD and CD (and BD and CD, of course).
As we have three right triangles, we can apply the Pythagorean Theorem to all three of them:
[1]
#" "AC^2 + BC^2 = AB^2# [2]
#" "AD^2 + CD^2 = AC^2# [3]
#" "BD^2 + CD^2 = BC^2#
Furthermore, you know that:
-
#AD# is#12# more than the altitude, so#AD = CD + 12# -
#BD# is#3# less than the altitude, so#BD = CD - 3#
Thus, you have
[4]
#" "AD = CD + 12# [5]
#" "BD = CD -3#
Last piece of information is that
[6]
#" "AB = AD + BD#
Now, let's try to find
First of all, let's plug [2] and [3] into [1]:
#color(blue)(AC^2)" " + color(green)(BC^2) " "= AB^2#
#=>" "(color(blue)(AD^2 + CD^2)) + (color(green)(BD^2 + CD^2)) = AB^2#
Now, let's use [6] and plug
#=>" "(AD^2 + CD^2) + (BD^2 + CD^2) = (color(brown)(AD + BD))^2#
Let's simplify this equation:
#=>" "AD^2 + BD^2 + 2CD^2 = (AD + BD)^2#
Use the formula
#=>" "AD^2 + BD^2 + 2CD^2 = AD^2 + 2*AD * BD + BD^2#
#=>" "cancel(AD^2) + cancel(BD^2) + 2CD^2 = cancel(AD^2) + 2*AD * BD + cancel(BD^2)#
#=> " " 2 * CD^2 = 2 * AD * BD#
Divide both sides by
#=> " " CD^2 = AD * BD#
Now, we can use [4] and [5]: plug
#=> " " CD^2 = color(orange)(AD) * color(purple)(BD)#
#=> " " CD^2 = (color(orange)(CD + 12)) * (color(purple)(CD - 3))#
Expand the right side:
#=> " " CD^2 = CD^2 + 9 CD - 36#
Subtract
#=> " " 0 = 9CD - 36#
Solve for
#=> " " CD = 4#
Thus, the altitude is
#AD = 4 + 12 = 16# #BD = 4 - 3 = 1# #AC = sqrt(AD^2 + CD^2) = sqrt(16^2 + 4^2) = sqrt(272)# #BC = sqrt(BD^2 + CD^2) = sqrt(1^2 + 4^2) = sqrt(17)# #AB = AD + BD = 16 + 1 = 17#
or
#AB = sqrt(AC^2 + BC^2) = sqrt(272+17) = 17#

