Question #22db6
3 Answers
I found
Explanation:
I would call the longer leg
Using Pythagoras we get:
so:
Using the Quadratic Formula:
so:
we use the positive one, giving the length of the longer length as
shorter leg = 5
Explanation:
Since this is a right triangle , we can use
#color(blue)" Pythagoras's theorem " # If h represents the hypotenuse and a , b the other 2 sides then
# h^2 = a ^2 + b^2# here , let the longer arm = x , so shorter one is then (x-7)
substitute values into formula :
hence
#13^2 = x^2 + (x-7)^2 = x^2 + x^2-14x + 49# so
#2x^2 - 14x + 49 = 169 # This is a quadratic function so equate to zero to solve.
#2x^2 - 14x - 120 = 0 # factorising:
#2(x^2 - 7x - 60 ) = 0 # To factor
#x^2-7x-60# require factors of -60 which sum to -7
These are 5 and - 12
#rArr 2(x-12)(x+5) = 0 rArr x = -5 , x = 12# now x > 0 hence x = 12 and so short leg = x-7 = 12 - 7 = 5
The length of shorter length is
Explanation:
Consider the diagram
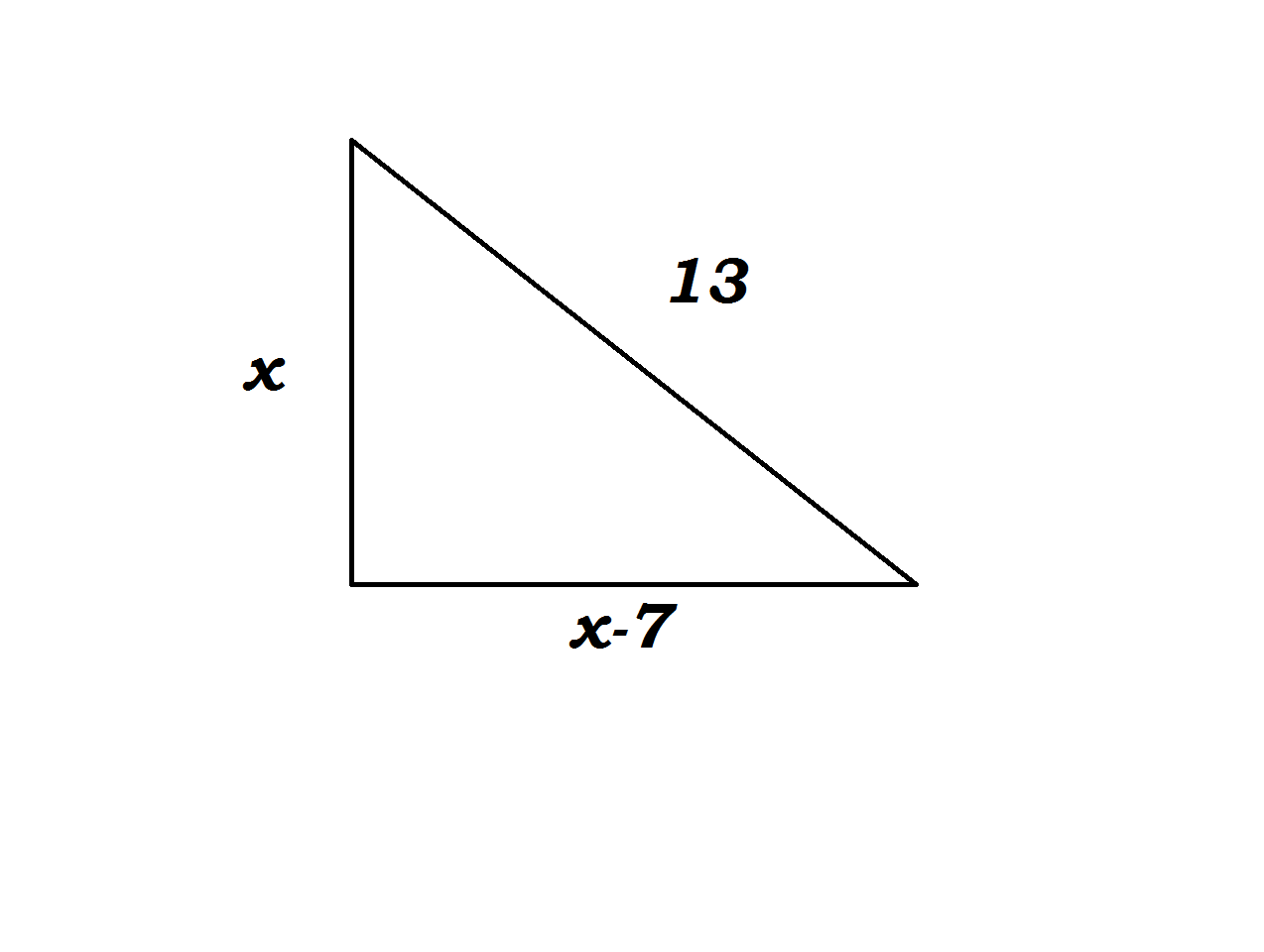
Use the pythagoras theorem
#color(brown)(x^2+y^2=h^2#
Where,
Use the formula
Factor it out
Remove the
If you solve for it you get,
#x=12,-5#
#x>0:.x=12#
#x=12,x-7=12-7=5#


