Question

MO diagram of `"B"_2"H"_6`?

Answer 1

I got the following two (blank) MO diagrams:

Bridging Boron-Hydrogen Interactions

Terminal Boron-Hydrogen Interactions

---

DISCLAIMER: This will be very long (and complicated). So long, in fact, that I will be separating the MO diagram into the terminal hydrogen interactions, and the bridging hydrogen interactions.

I have also omitted some of the work for which representative examples are already in the answer.

As an overview of what I will be doing:

1. Symmetry of `"B"_2"H"_6`: Point Group
2. Symmetry of `"B"_2"H"_6`: Character Table
3. Reducible Representations for the two borons, and reducing them to their irreducible representations
4. Irreducible Representations for the terminal hydrogen interactions (just the results), and the MO diagram for terminal hydrogen interactions (not elaborated on in my textbook)
5. Irreducible Representations for the bridging hydrogen interactions (just the results), and the MO diagram for bridging hydrogen interactions (mentioned in my textbook)

(As I do not know how the relative molecular orbital energies actually compare for the molecule as a whole, I will leave these two MO diagrams separate.)

I will be using a vector projection method to determine which orbitals can interact and in what way.

POINT GROUP OF B2H6

Before we get into the MOs and whatnot, since my textbook assumes a lot, we have to establish how `"B"_2"H"_6` is categorized, so we can determine which orbitals, in layman's terms, are indicated by each non-layman symmetry label.

The structure of `"B"_2"H"_6` and its coordinate system looks like this:

The bridging `"B"-"H"-"B"` bond shares 2 electrons. Each terminal `"B"-"H"` bond contains 2 electrons. This accounts for 12 total valence electrons in `"B"_2"H"_6`.

Now, if we imagine the symmetry elements that are present in this molecule, we get the following:

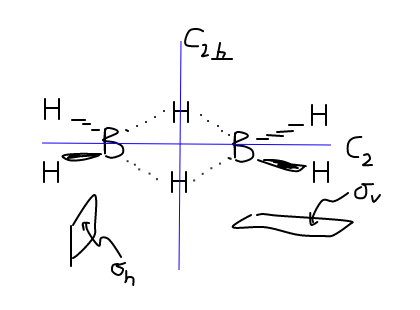
There are others, but the bare minimum we need to ascertain the point group is:

• `"C"_2` axis. This is known as the principal rotation axis, where if you rotate `(360^@)/2 = 180^@`, you return the same molecule back.
• `sigma_v (yz)` is the vertical reflection plane, which is colinear with the `C_2` principal axis. When you reflect `"B"_2"H"_6` through this `yz`-plane, you get the same molecule back.
• `sigma_h (xy)` is the horizontal reflection plane, which is perpendicular with the `C_2` principal axis. When you reflect `"B"_2"H"_6` through this `xy`-plane, you get the same molecule back.
• Note that we also have a `sigma_v' (xz)` plane, which we will also use.
• `"C"_(2,_|_)` is the same kind of axis, but it is the rotation axis perpendicular to the `"C"_2` axis. It is this axis that will confirm which point group we are looking for.

Based on the above symmetry analysis, we are looking at what's called the `\mathbf("D"_(2h))` point group, which requires at least one `"C"_2`, one `"C"_(2,_|_)`, and one `sigma_h` symmetry element.

The reason why we needed to figure this out is because we are trying to categorize each orbital in the molecule, and these categories, called irreducible representations (IRREPs), are different for each point group.

CHARACTER TABLE

The `"D"_(2h)` point group has associated with it a character table, which we can use to determine each IRREP.

I realize this is quite big, but it is a complex molecule. Let's work through this.

The equation we'll need to repeatedly use along with this table is:

`\mathbf(Gamma_"IRREP" = 1/h sum_("elements") n_(hatR) Gamma_("basis") chi_(hatR)^"irrep")`

`\mathbf(Gamma_"basis"^"red." = sum_(i=1)^("IRREPs") "IRREP" _((i))*Gamma_("IRREP"(i)))`

where:

• `Gamma_"basis"^"red."` is the irreducible representation. It gives the "scaled-down" results of performing each symmetry operation (reflection, inversion, rotation, identity).
• The "IRREPs" will be `A_g`, `B_(1g)`, . . . , `B_(3u)`.
• `hatR` is each symmetry operation (`hatE`, `hatC_2(z)`, `hatC_2(y)`, etc).
• `h` is the order of the point group, and is found from summing the coefficients on each symmetry element. For this we will get `1+1+1+1+1+1+1+1 = color(blue)(8)`.
• `n_(hatR)` is the coefficient next to each symmetry operation (next to `hatE`, `hatC_2(z)`, `hatC_2(y)`, etc). This is `1` in this case for all operations.
• `Gamma_("basis")` is the reducible representation. The "basis" will be either the `2s`, `2p_x`, `2p_y`, or `2p_z` orbitals of boron, or the `1s` orbitals of hydrogen. So, we'll be running over six bases! Yowza.
• `chi_(hatR)^"IRREP"` is each number for a given row in the character table. For example, in `A_u` you would use `1`, `1`, `1`, `1`, `-1`, `-1`, `-1`, and then `-1`.

Keep this in mind, as we'll be going back and using this table and this equation 48 times!!! (6 bases and 8 IRREPs)

REDUCIBLE REPRESENTATIONS FOR THE TWO BORONS

Okay, to find `Gamma_"basis"`, the reducible representation, for the two borons, we have the four bases to consider: `2s`, `2p_x`, `2p_y`, and `2p_z`.

For this, we have the following guidelines after each operation:

• If nothing happens to an orbital, it returns `1`.
• If the sign changes for the orbital, it returns `-1`.
• If the orbital has been moved from its place (such as if one orbital takes the place of a different orbital), then it returns `0`.

Each operation works as follows:

• `hatE` returns the same orbitals back.
• `hatC_2(z), hatC_2(y), hatC_2(x)` rotate the orbitals `180^@` about the `z`, `y`, and `x` axis, respectively.
• `hati` inverts the orbitals, so that we have `(x,y,z) -> (-x,-y,-z)`. For this entire answer, you will return `0` for this operation.
• `hatsigma` reflects the orbitals through the indicated plane. If the orbitals lie along the plane, nothing happens. If they lie on either side of the plane, they will get moved from their place.

If you go through all these operations for the boron atoms, then for each basis you should get:

`Gamma_(2s,2xx"B") = color(white)([(color(black)(hat"E"), color(black)(hat"C"_2(z)), color(black)(hat"C"_2(y)), color(black)(hat"C"_2(x)), color(black)(hati), color(black)(hatsigma(xy)), color(black)(hatsigma(xz)), color(black)(hatsigma(yz))),(color(black)(2),color(black)(2),color(black)(0),color(black)(0),color(black)(0),color(black)(0),color(black)(2),color(black)(2))])`

`Gamma_(2p_x,2xx"B") = color(white)([(color(black)(hat"E"), color(black)(hat"C"_2(z)), color(black)(hat"C"_2(y)), color(black)(hat"C"_2(x)), color(black)(hati), color(black)(hatsigma(xy)), color(black)(hatsigma(xz)), color(black)(hatsigma(yz))),(color(black)(2),color(black)(-2),color(black)(0),color(black)(0),color(black)(0),color(black)(0),color(black)(2),color(black)(-2))])`

`Gamma_(2p_y,2xx"B") = color(white)([(color(black)(hat"E"), color(black)(hat"C"_2(z)), color(black)(hat"C"_2(y)), color(black)(hat"C"_2(x)), color(black)(hati), color(black)(hatsigma(xy)), color(black)(hatsigma(xz)), color(black)(hatsigma(yz))),(color(black)(2),color(black)(-2),color(black)(0),color(black)(0),color(black)(0),color(black)(0),color(black)(-2),color(black)(2))])`

`Gamma_(2p_z,2xx"B") = color(white)([(color(black)(hat"E"), color(black)(hat"C"_2(z)), color(black)(hat"C"_2(y)), color(black)(hat"C"_2(x)), color(black)(hati), color(black)(hatsigma(xy)), color(black)(hatsigma(xz)), color(black)(hatsigma(yz))),(color(black)(2),color(black)(2),color(black)(0),color(black)(0),color(black)(0),color(black)(0),color(black)(2),color(black)(2))])`

This reduces as follows. I'll do one of them, and infer off of that one.

`2s` orbitals of boron:

Only the first two and last two numbers are nonzero, so let's only examine the first two and last two columns for each row.

`color(blue)(Gamma_(A_g)) = 1/8[1*2*1 + 1*2*1 + 1*0*1 + 1*0*1 + 1*0*1 + 1*0*1 + 1*2*1 + 1*2*1] = color(blue)(1)`

`Gamma_(B_(1g)) = 1/8[1*2*1 + 1*2*1 + . . . + 1*2*(-1) + 1*2*(-1)] = 0`
`Gamma_(B_(2g)) = 1/8[1*2*1 + 1*2*(-1) + . . . + 1*2*1 + 1*2*(-1)] = 0`
`Gamma_(B_(3g)) = 1/8[1*2*1 + 1*2*(-1) + . . . + 1*2*(-1) + 1*2*1] = 0`
`Gamma_(A_u) = 1/8[1*2*1 + 1*2*1 + . . . + 1*2*(-1) + 1*2*(-1)] = 0`
`color(blue)(Gamma_(B_(1u))) = 1/8[1*2*1 + 1*2*1 + . . . + 1*2*1 + 1*2*1] = color(blue)(1)`
`Gamma_(B_(2u)) = 1/8[1*2*1 + 1*2*(-1) + . . . + 1*2*(-1) + 1*2*1] = 0`
`Gamma_(B_(3u)) = 1/8[1*2*1 + 1*2*(-1) + . . . + 1*2*1 + 1*2*(-1)] = 0`

Using the `2s` orbitals as an example, the results for the IRREPS from the above calculations for the orbitals of the two borons are:

• `color(blue)(Gamma_(2s,2xx"B")^"red.") = A_g*Gamma_(A_g) + B_(1u)*Gamma_(B_(1u)) = color(blue)(A_g + B_(1u))`
• `color(blue)(Gamma_(2p_x,2xx"B")^"red.") = B_(2g)*Gamma_(B_(2g)) + B_(3u)*Gamma_(B_(3u)) = color(blue)(B_(2g) + B_(3u))`
• `color(blue)(Gamma_(2p_y,2xx"B")^"red.") = B_(3g)*Gamma_(B_(3g)) + B_(2u)*Gamma_(B_(2u)) = color(blue)(B_(3g) + B_(2u))`
• `color(blue)(Gamma_(2p_z,2xx"B")^"red.") = A_g*Gamma_(A_g) + B_(1u)*Gamma_(B_(1u)) = color(blue)(A_g + B_(1u))`

The physical representation of these is as follows:

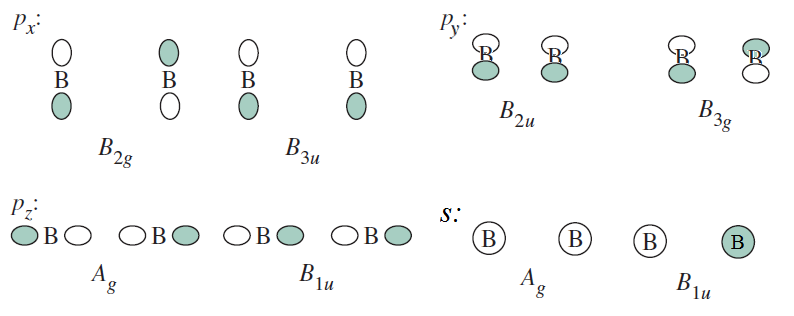
(Book shows `p_x`, `p_z`, and `s`, but I had to derive `p_y`.)

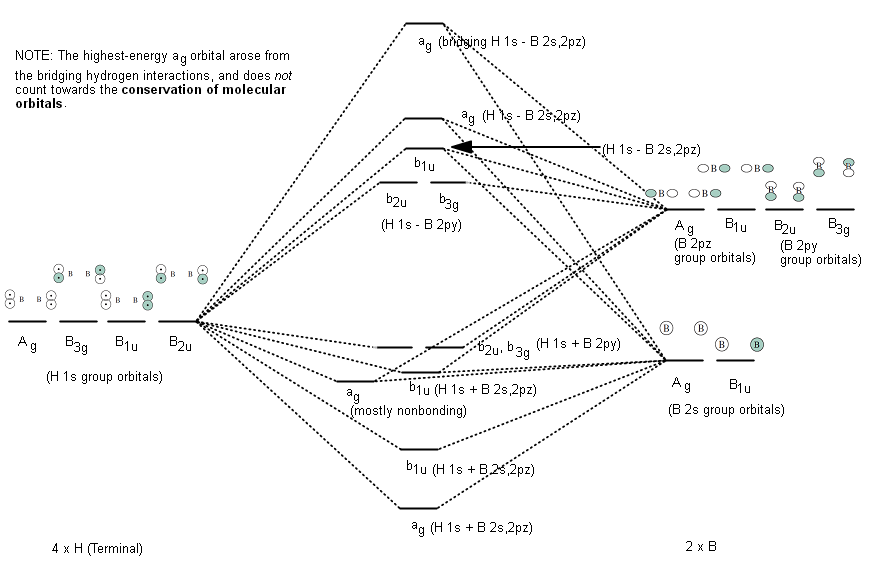
IRREDUCIBLE REPRESENTATIONS FOR THE TERMINAL HYDROGENS

Using similar operations as above for `Gamma_"basis"`, the resultant physical representations of the IRREPs are:

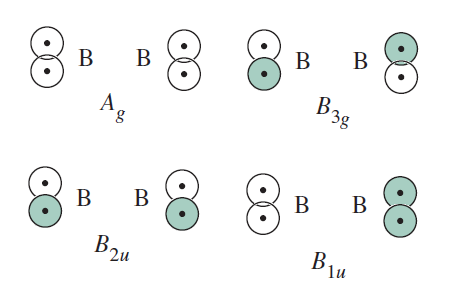
This (eventually) gives the following MO diagram:

There would be 8 valence electrons in this diagram (2 each in the lowest two `a_g` orbitals and 2 each in the lowest two `b_(1u)` orbitals).

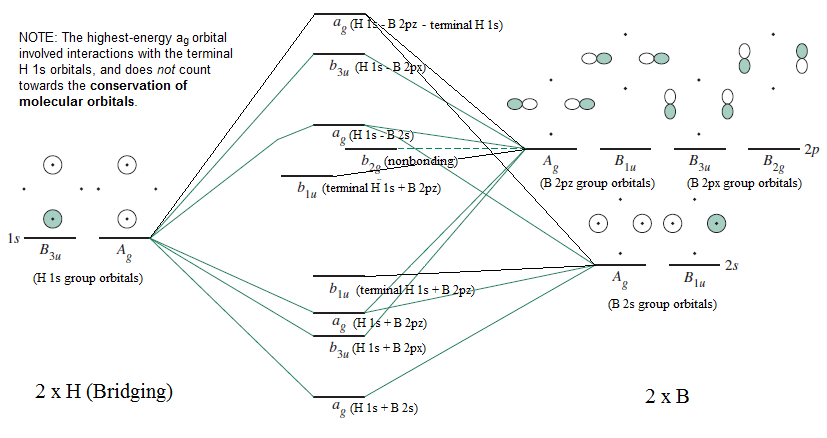
IRREDUCIBLE REPRESENTATIONS FOR THE BRIDGING HYDROGENS

Using similar operations as above for `Gamma_"basis"`, the resultant physical representations of the IRREPs are:

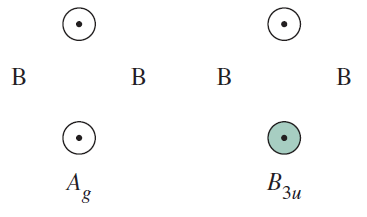
My book shows the MO diagram for the bridging interactions in `"B"_2"H"_6`, but it neglects to include the influence of the terminal hydrogen orbital interactions with the boron orbitals (it does mention it, but does not incorporate the information into the images).

I'll still leave the MO diagrams separate, but I've slightly modified the MO diagram from my book to account for these interactions, and to annotate it.

There would be 4 valence electrons in this diagram (2 in the lowest `a_g` orbital and 2 in the lowest `b_(3u)` orbital).