Question #8f49b
1 Answer
Explanation:
The trick here is to focus on how the concentration of the target solution relates to the concentration of the initial solution.
You don't have to know the exact values of the two concentrations, all you need to know is that
#"N"/2 xx 1/color(red)(5) = "N"/10#
This means that the concentration of the target solution decreased by a factor of
Now, the key to any dilution calculation is the fact that when you're diluting a solution, the number of moles of solute remains unchanged.
In other words, you can decrease the concentration of a solution by increasing its volume, while at the same time keeping the number of moles of solute constant.
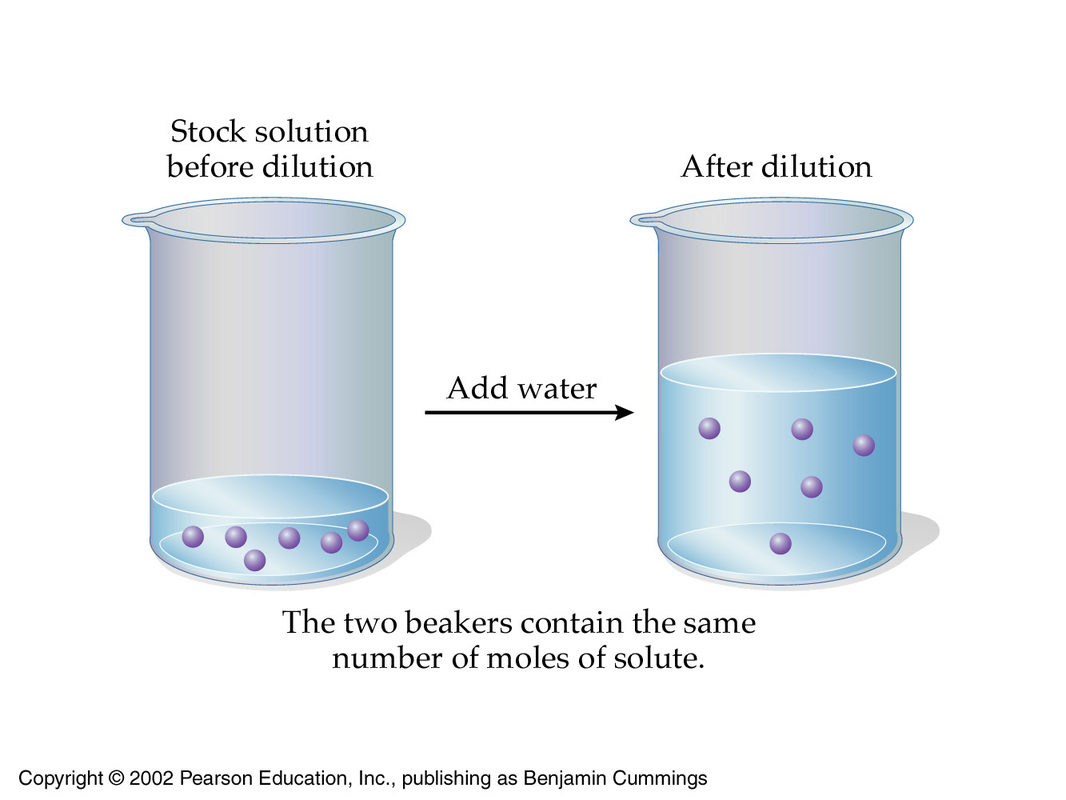
This means that in order for the concentration of a solution to decrease by a factor of
Therefore, the volume of the target solution must be
#V_"target" = color(red)(5) xx "150 mL" = "750 mL"#
This means that you must add
#V_"water" = "750 mL" - "150 mL" = color(green)(|bar(ul(color(white)(a/a)color(black)("600 mL")color(white)(a/a)|)))#
of water to your initial solution to get its concentration to drop from
Mathematically, this can be shown by using the equation for dilution calculations
#color(blue)(overbrace(c_1 xx V_1)^(color(darkgreen)("moles of solute in concentrated solution")) = overbrace(c_2 xx V_2)^(color(darkgreen)("moles of solute in diluted solution"))#
Here
Rearrange to solve for
#c_1 * V_1 = c_2 * V_2 implies V_2 = c_1/c_2 * V_1#
Plug in your values to find
#V_2 = color(red)(cancel(color(black)("N")))/2 * 10/color(red)(cancel(color(black)("N"))) * "150 mL" = "750 mL"#
Once again ,the volume of water that must be added is
#V_"water" = "750 mL" - "150 mL" = color(green)(|bar(ul(color(white)(a/a)color(black)("600 mL")color(white)(a/a)|)))#

