Question #69a7c
1 Answer
Explanation:
The underlying principle behind a dilution is that the number of moles of solute present in the concentrated solution must be equal to the number of moles of solute present in the diluted solution.
In essence, a dilution decreases the concentration of the solution by increasing its volume while keeping the number of moles of solute constant.
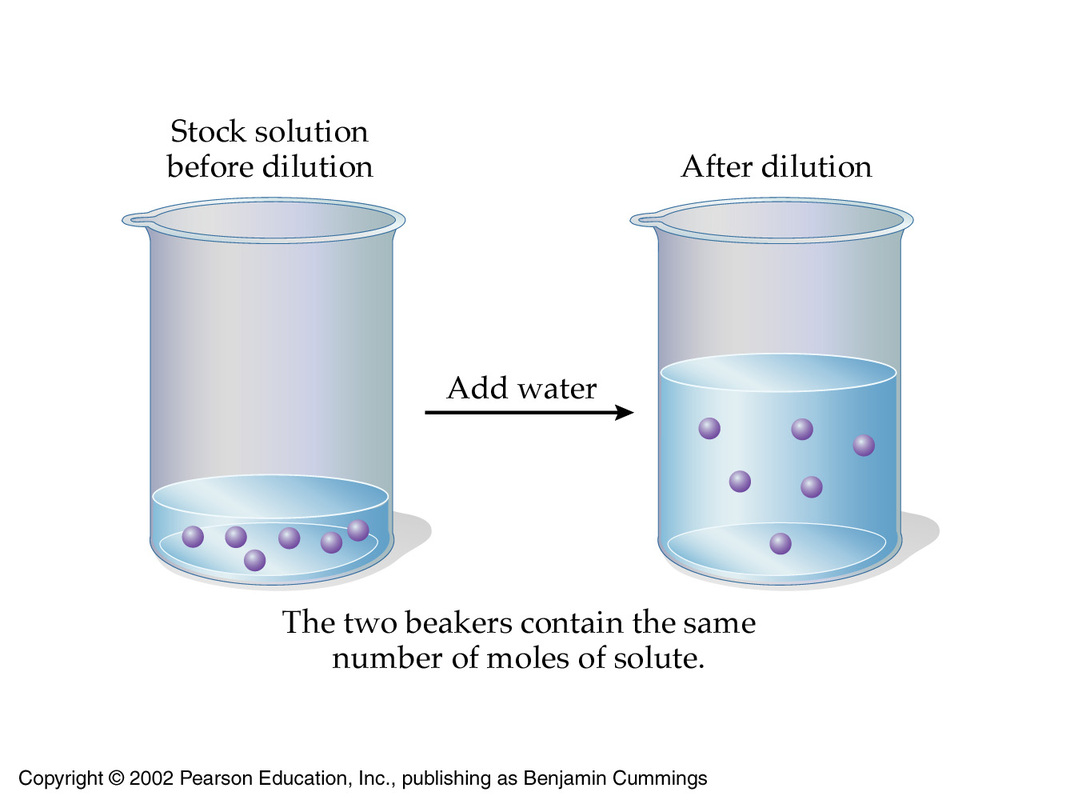
As you know, the number of moles of solute can be expressed using the molarity and volume of the solution
#color(purple)(|bar(ul(color(white)(a/a)color(black)(c = n_"solute"/V_"solution" implies n_"solute" = c * V_"solution")color(white)(a/a)|)))#
The number of moles of sodium nitrate,
#c_(NaNO_3) = "0.512 mol" color(red)(cancel(color(black)("L"^(-)))) * 25 * 10^(-3)color(red)(cancel(color(black)("L"))) = "0.0128 moles NaNO"_3#
This is exactly how many moles of sodium nitrate must be present in the diluted solution. This means that you have
#c_"diluted" = "0.0128 moles"/(225 * 10^(-3)"L") = color(green)(|bar(ul(color(white)(a/a)"0.057 M"color(white)(a/a)|)))#
The answer is rounded to two sig figs.
ALTERNATIVE APPROACH
Another way to approach this problem is by using the formula for dilution calculations, which looks like this
#color(blue)(overbrace(c_1 xx V_1)^(color(black)("moles of solute in concentrated solution")) = overbrace(c_2 xx V_2)^(color(black)("moles of solute in diluted solution"))#
Here you have
Rearrange to solve for
#c_1V_1 = c_2V_2 implies c_2 = V_1/V_2 * c_1#
Plug in your values to get
#c_2 = (25 color(red)(cancel(color(black)("mL"))))/(225color(red)(cancel(color(black)("mL")))) * "0.512 M" = color(green)(|bar(ul(color(white)(a/a)"0.057 M"color(white)(a/a)|)))#

