What is the geometry and hybridization of #"PF"_6^(-)#? What orbitals are used to hybridize?
1 Answer
In general, the typical pattern for basic/simple molecules is:
- Diatomic molecule
#=># No hybridization at all! (EX:#"HCl"# ) - 2 electron groups
#=># #sp# hybridization (EX:#"CO"_2# ) - 3 electron groups
#=># #sp^2# hybridization (EX:#"BF"_3# ) - 4 electron groups
#=># #sp^3# hybridization (EX:#"CH"_4# ) - 5 electron groups
#=># #sp^3d# hybridization (EX:#"PF"_5# ) - 6 electron groups
#=># #sp^3d^2# hybridization (EX:#"SF"_6# )
You can count these up and see that the number of orbitals used in the hybridization equal the number of electron groups around the central atom.
HYPERVALENCY OF PHOSPHORUS
Since phosphorus (
That means it can use its
This generates an octahedral molecular and electron geometry. You can see the final shape of this at the bottom.
PRINCIPLES OF ORBITAL HYBRIDIZATION
Orbital hybridization in
(The ideal bond angles are a separate phenomenon based on electron repulsions.)
For example, an overlap between two
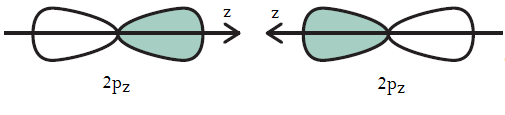
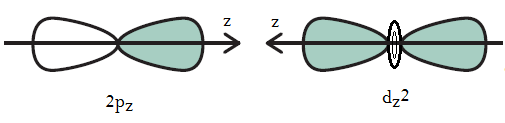
The problem is that they should be the same bonds for a molecule making six identical
GENERATING THE HYBRIDIZED ORBITALS
To make the bonds more uniform, hybridization must occur between the
Then, what you will have is six sets of
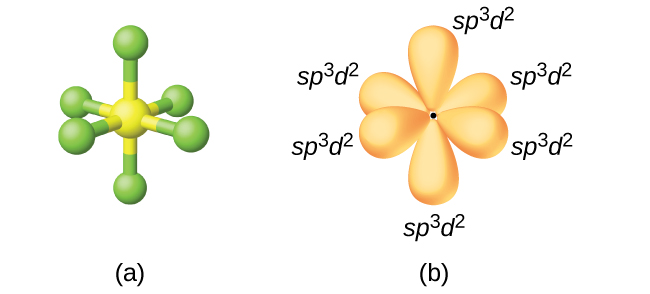 http://chemwiki.ucdavis.edu/
http://chemwiki.ucdavis.edu/
You can see the adjacent bond angles are all

