Question #e7ecb
1 Answer
Explanation:
The trick here is to realize that when you're working with gases kept under the same conditions for pressure and temperature, which seems to be the case here, the mole ratio that exists between the gases is equivalent to a volume ratio.
When pressure and temperature are kept constant, let's say
#P * V_(HF) = n_(HF) * RT -># for hydrogen fluoride
#P * V_(N_2F_2) = n_(N_2F_2) * RT -># for dinitrogen difluoride
#P * V_"product" = n_"product" * RT -># for the product of the reaction
You can thus get the mole ratio that exists between the gases by dividing these equations. For example, the two reactants will have
#(color(red)(cancel(color(black)(P))) * V_(HF))/(color(red)(cancel(color(black)(P))) * V_(N_2F_2)) = (n_(HF) * color(red)(cancel(color(black)(RT))))/(n_(N_2F_2) * color(red)(cancel(color(black)(RT))))#
which is equivalent to saying that
#color(purple)(|bar(ul(color(white)(a/a)color(black)(n_(HF)/n_(N_2F_2) = V_(HF)/V_(N_2F_2))color(white)(a/a)|))) -># the mole ratio is equivalent to the volume ratio
This means that the two reactants will react in a
#n_(HF)/n_(N_2F_2) = (10 color(red)(cancel(color(black)("cm"^3))))/(5color(red)(cancel(color(black)("cm"^3)))) = 2/1#
Notice that the reaction produces
You can thus say that you have
#color(red)(2)"HF"_ ((g)) + "N"_ 2"F"_(2(g)) -> color(red)(2) xx color(blue)("product")#
Now all you have to do is count the atoms that are present on the reactants' side and make sure that you add them to the products' side as well.
The reactants' side contains
The chemical equation will thus be
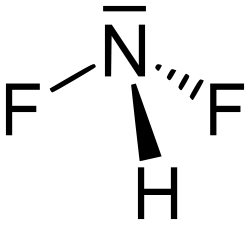
#color(red)(2)"HF"_ ((g)) + "N"_ 2"F"_ (2(g)) -> color(red)(2)"NHF"_(2(g))#
The product of the reaction is called difluoramine.