Question

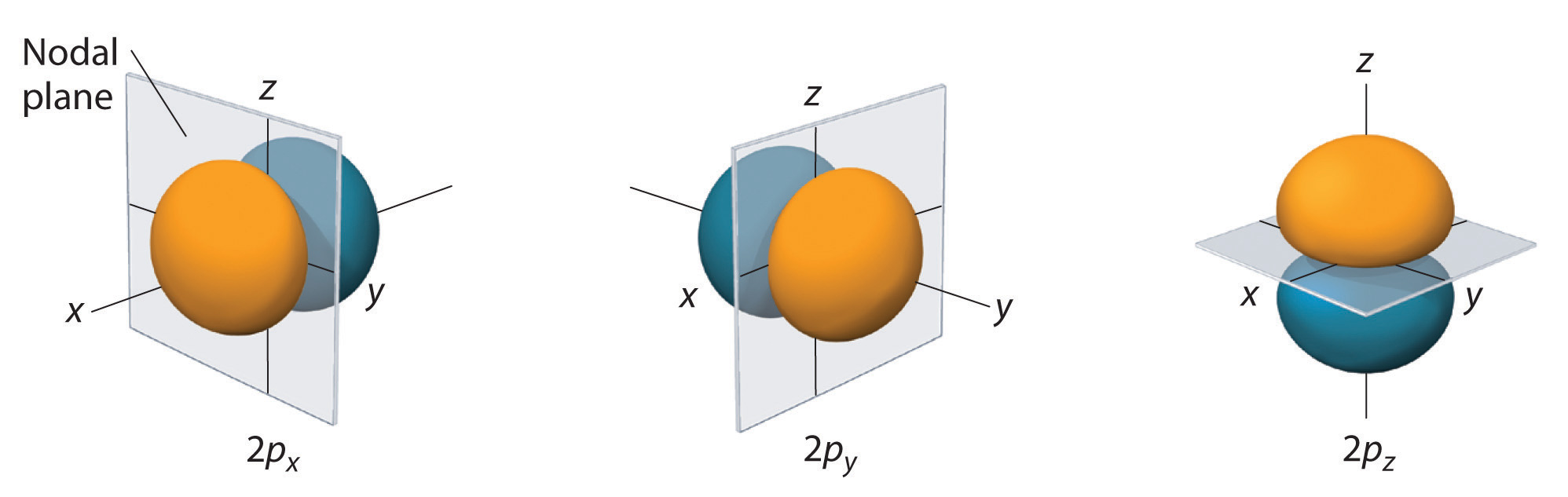
What is the formula for calculating a nodal point?

Answer 1

There is none. You need the wave function for the particular orbital, which is not readily available unless the atom is hydrogen...

---

In the case of hydrogenic atoms, i.e. one-electron atoms, the wave functions are available in most physical chemistry textbooks up through `n = 3`.

As a simple but not undercomplicated example, consider one of the `2p` orbitals:

The hydrogenic atom wave function for the `2p_z` is:

`psi_(2pz) = R_(21)(r)Y_(1)^(0)(theta,phi)`

`= 1/(4sqrt(2pi)) (Z/a_0)^(3//2) sigmae^(-sigma//2)costheta`,

where:

• `sigma = Zr//a_0`.
• `Z` is the atomic number.
• `a_0 = "0.0529177 nm"` is the Bohr radius.
• `r` is the radial distance away from the nucleus.
• `R_(nl)(r)` is the radial component of the wave function.
• `Y_(l)^(m_l)(theta,phi)` is the angular component of the wave function.

The radial nodes are where `R_(nl)(r) = 0`, and the angular nodes are where `Y_(l)^(m_l)(theta,phi) = 0`.

Since nonzero constants are clearly never zero, we just have to pick out the functions that have `r` or `theta`. That is, we just need the fact that:

`R_(21)(r) prop sigmae^(-sigma//2)`

`Y_(1)^(0)(theta,phi) prop costheta`

RADIAL NODES?

So, solving for the radial nodes, with `sigma = Zr//a_0`:

`(Zr)/(a_0)e^(-Zr//2a_0) = 0`

This exponential never goes to zero except at `oo`, at which the orbital doesn't exist, so we can eliminate it.

`=> (Zr)/(a_0) = 0`

From here we can realize that there are no radial nodes in the `2p_z` orbital.

The only solution to this is `r = 0`, and at `r = 0`, no electrons exist because there is no electron that can fit in a radius of `"0 meters"`.

ANGULAR NODES?

Solving for the angular nodes,

`costheta = 0`

And this only nonredundantly applies for `theta in [0,pi]`.

So, in this domain, `costheta = 0` at `theta = pi/2`, or `90^@`, relative to the axis of the orbital (the `z` axis).

Furthermore, there is no `phi` dependence, so integration over the `phi` variable to generate this orbital probability density contributes only a constant of `2pi`:

`"Probability Density of 2p"_z`

`= int_(0)^(2pi) int_(0)^(pi) int_(0)^(oo) psi_(2pz)^"*"psi_(2pz)r^2dr sinthetad theta d phi`

`= color(red)(1/(4sqrt(2pi)) (Z/a_0)^(5) int_(0)^(2pi) d phi) int_(0)^(pi) cos^2theta sintheta d theta int_(0)^(oo) r^2e^(-Zr//a_0)dr`

`= color(red)((2pi)/(4sqrt(2pi))(Z/a_0)^(5)) int_(0)^(pi) cos^2theta sintheta d theta int_(0)^(oo) r^2e^(-Zr//a_0)dr`

Having no dependence on the value of `phi` for a wave function that goes to zero at a particular value of `theta` means that a nodal plane is generated.

Therefore, the angular node is a plane perpendicular to the `z` axis of the `2p_z` orbital, and is the `xy` plane, just like it shows in the above diagram.