Question #dd7e8
1 Answer
Explanation:
The trick here is to realize that when volume and number of moles of gas are kept constant, pressure and temperature have a direct relationship as described by Gay Lussac's Law.
In other words, when volume and number of moles are constant, increasing a gas' temperature will cause its pressure to increase, and decreasing the gas' temperature will cause its pressure to decrease.
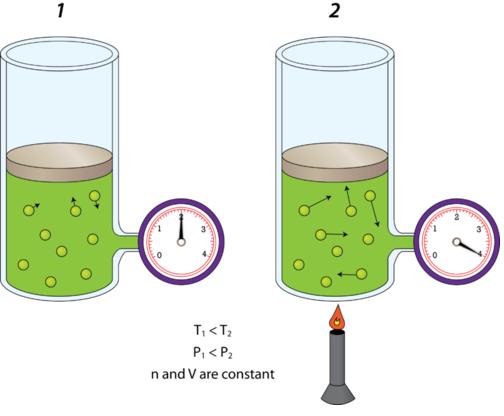
In your case, the temperature of the gas increases from
Mathematically, Gay Lussac's Law can be written as
#color(blue)(|bar(ul(color(white)(a/a)P_1/T_1 = P_2/T_2color(white)(a/a)|)))" "# , where
Rearrange the equation to solve for
#P_1/T_1 = P_2/T_2 implies P_2 = T_2/T_1 * P_1#
Plug in your values to find
#P_2 = (684 color(red)(cancel(color(black)("K"))))/(428color(red)(cancel(color(black)("K")))) * "86 atm" = color(green)(|bar(ul(color(white)(a/a)color(black)("140 atm")color(white)(a/a)|)))#
The answer is rounded to two sig figs, the number of sig figs you have for the initial pressure of the gas.

