Question

How to show that `["Co"("CN")_6]^(3-)` (a yellow complex) has a larger `Delta_o` than `["CoF"_6]^(3-)` (a blue complex) using knowledge of `sigma` donor, `pi` donor, and `pi` acceptor behavior, and spin-only magnetic moment?

Answer 1

First of all, it is crucial to recognize the following:

• The crystal field splitting energy (i.e. the `Delta_o` for these octahedral complexes) corresponds to the energy of the light absorbed.
• The color of the complexes is due to light reflected, so the complementary color is absorbed and its wavelength is what we should compare.

PI DONORS, SIGMA DONORS, AND PI ACCEPTORS

Now, recall what it means to be a `bbpi` donor, `bbsigma` donor, and `bbpi` acceptor.

• `pi` donors donate electron density into the metal's bonding `pi` orbitals. This somewhat raises the energy of the `bb(t_(2g))` orbitals.
• `sigma` donors donate electron density into the metal's antibonding `sigma^"*"` orbitals. This raises the energy of the `bb(e_g)` orbitals.
  
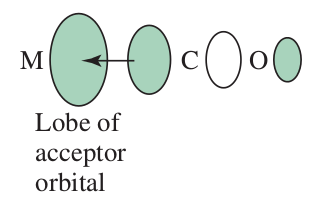
• `pi` acceptors accept electron density from the metal bonding `pi` orbitals. This lowers the energy of the `bb(t_(2g))` orbitals.
  
  The `pi` donation depiction is similar, but in reverse.

These energy alterations are summarized below, using `["CrF"_6]^(3-)` and `["Cr"("CN")_6]^(3-)` as examples of a strong-field and weak-field splitting, respectively:

From left to right you can see `Delta_o` decreasing.

Therefore, `pi` acceptors are the strongest-field ligands (large crystal field splitting energy, promotes low-spin), and `pi` donors are the weakest-field ligands (small crystal field splitting energy, promotes high-spin).

WAVELENGTH CONCLUSIONS

As it turns out, `"CN"^(-)` is a great `pi` acceptor AND `sigma` donor, so its `Delta_o` should be large, compared to that from `"F"^(-)`, a `pi` donor.

From this, it follows that the `Delta_o` for `["CoF"_6]^(3-)` is smaller than that for `["Co"("CN")_6]^(3-)`, and thus corresponds to a smaller frequency and longer wavelength.

Given that...

• blue reflected light corresponds to orange absorbed light,
• and yellow reflected light corresponds to violet absorbed light,

...we have that violet light is lower wavelength, violet is higher frequency and thus the yellow complex should have a larger `Delta_o` and stronger-field ligand... and it does!

SPIN-ONLY MAGNETIC MOMENT?

Lastly, the exact spin-only magnetic moment equation is not important for this purpose. All it really gives us for this situation is that higher `mu_S` corresponds to more unpaired electrons.

The point is to realize that that strong-field ligands give rise to low-spin complexes (more electron pairing), and vice versa.

Therefore, we expect that `["Co"("CN")_6]^(3-)` has a lower `mu_S` than `["CoF"_6]^(3-)`, as the former has less unpaired electrons than the latter. This would experimentally demonstrate that `"CN"^(-)` is strong-field and `"F"^(-)` is weak-field.