Question

Question #66e6d

Answer 1

The answer is (3) `27`

Explanation:

The idea here is that the temperature coefficient, which you'll sometimes see referred to as the `Q_(10)` coefficient, relates the change in the rate of a reaction to a `10^@"C"` increase in the temperature of the reaction.

Simply put, the `Q_(10)` coefficient tells you how increasing the temperature of the reaction by `10^@"C"` will affect its rate.

The equation that allows you to calculate the `Q_(10)` coefficient looks like this

`color(blue)(|bar(ul(color(white)(a/a)Q_(10) = ("rate"_2/"rate"_1)^(10/(T_2 - T_1))color(white)(a/a)|)))`

Here

`T_1` - the initial absolute temperature of the reaction
`T_2` - the new absolute temperature of the reaction
`"rate"_1` - the rate at `T_1`
`"rate"_2` - the rate at `T_2`

Now, a `Q_(10)` coefficient of `3` means that with every `10^@"C"` increase in temperature, the rate of the reaction increases by a factor of `3`.

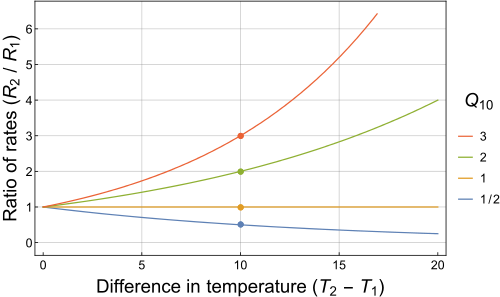
It's important to notice that because you're dealing with change in temperature, you can skip the conversion to Kelvin.

That is the case because an increase by `1^@"C"` is equal to an increase by `"1 K"`.

So in the case of a `10^@"C"` increase, you would have

`T_2 - T_1 = "10 K"`

and

`Q_(10) = ("rate"_2/"rate"_1)^(10/10) = "rate"_2/"rate"_1`

In your case,

`3 = "rate"_2/"rate"_1 implies color(purple)(|bar(ul(color(white)(a/a)color(black)("rate"_2 = 3 xx "rate"_1)color(white)(a/a)|)))`

For your reaction, the temperature goes from `35^@"C"` to `65^@"C"`. This is equivalent to

`DeltaT = 65^@"C" - 35^@"C" = 30^@"C"`

So, if the rate of the reaction increases by factor of `3` with every `10^@"C"` increase in temperature, it follows that a

`30^@"C" = 3 xx 10^@"C"`

increase will cause the rate to go up by

`"rate"_2 = overbrace(color(white)(aaa)3color(white)(aaa))^(color(darkgreen)("for a 10"^@"C increase")) xx overbrace(color(white)(aaa)3color(white)(aaa))^(color(darkgreen)("for a 10"^@"C increase")) xx overbrace(color(white)(aaa)3color(white)(aaa))^(color(darkgreen)("for a 10"^@"C increase")) xx "rate"_1`

`"rate"_2 = 27 xx "rate"_1`

Therefore, the rate of the reaction will increase by a factor of `27`.