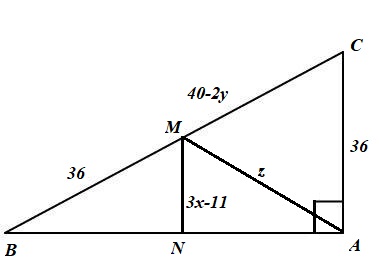
In the #DeltaABC# below, #M# and #N# are midpoints of #BC# and #AB# respectively, #m/_A=90^@#. Find #x,y# and #z#?
1 Answer
Jul 6, 2016
Explanation:
As M is the midpoint of BC, we have
As
As
Hence,
