Question

What is the hybridization and symmetry of `["Cu"_2"Cl"_8]^(4-)`?

Answer 1

I got its symmetry as `C_(2h)`. Read further in the answer for the hybridization explanation.

---

DISCLAIMER: Kind of long answer.

I think you are asking about `["Cu"_2"Cl"_8]^(4-)`. I found a paper about it. It's actually quite short, so you should check it out.

A similar compound is `(mu_2-"CO")_2"Co"_2("CO")_6`, dicobalt octacarbonyl:

(`mu_2` means it is bridging with two atoms at the same time.)

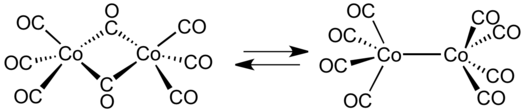
Similarly, dicopper octachloride anion, `["Cu"_2"Cl"_8]^(4-)` looks like this:

ORBITAL "HYBRIDIZATION"

It's not easy to say what its hybridization is.

The paper states it is a distorted trigonal bipyramidal molecular geometry around the copper with "one axial and one equatorial chlorine" atoms bridging the two not-bonded copper atoms. One could say it is `sp^3d`, but I doubt that it is sufficient to describe this.

Assuming the `"Cu"-"Cu"` distance is the `x`-axis, and the plane of the paper/screen is the `xy`-plane, we have the `z` axis coming out towards us, and:

• The bridging chlorine atoms can be said to each use their `3p_x` atomic orbital to bond with each copper's `3d_(xy)` orbitals.
• Probably, each chlorine can use its `3p_z` orbital for some weak `pi`-bonding with the coppers' `3d_(yz)` orbitals (two-lobe same-sign overlap of the `d` orbital's top two lobes).

Below I've depicted the `3p_x-3d_(xy)` interaction for the bonding molecular orbital overlap:

As the configuration of each copper and its respective three terminal chlorine atoms resembles `"NH"_3`, the isolated `"CuCl"_3` portions can be called a "trigonal pyramidal shape" (but don't just call the whole molecule that!).

POINT GROUP SYMMETRY

As for the symmetry (which I'm assuming means point group symmetry), we can start from thinking about the molecule from a different angle.

PRINCIPAL AXIS

First, find the principal axis. By convention that is the z-axis as well.

If you look down the `"Cu"-"Cu"` line of sight, you should see the three chlorines `120^@` apart, just as you would for the hydrogens in `"NH"_3` when looking through the `"N"` from below.

Unfortunately the bridging chlorines break that symmetry.

The alternative is the axis through the plane of the screen, which rotates the molecule, the whole time remaining upon the plane of the screen - that is a `C_2` axis, because it requires a `360^@/2 = 180^@` rotation, where `n = 2`.

MIRROR/REFLECTION PLANES

Next, you should consider whether the molecule has a mirror plane (at least one coplanar, and possibly one perpendicular to the principal axis).

In fact, it does.

• The `(mu_2-"Cl")_2"Cu"_2` plane (the plane of the depicted orbital overlap) is a horizontal reflection plane, `sigma_h`, because it is perpendicular with the `z`-axis, and it is labeled `sigma_h` to indicate that

• Since this molecule is staggered in its most stable form, it does not have a vertical mirror plane, `sigma_v`, intersecting the bridging `"Cl"` atoms and bisecting the left/right halves of the molecule.

POINT OF INVERSION

Another thing to consider is that it has a center of inversion, `i`. That means if you swap the positions of all atoms with the atom opposite to them, you return the same molecule.

So, you reflect through the `yz`-plane, and then the `xz`-plane and then the `xy`-plane. If the same molecule is returned, then you have your center of inversion.

PUTTING IT ALL TOGETHER

Now, for these reasons:

• The principal axis is a `C_(color(red)(2))` axis.
• There is a `sigma_color(red)(h)` horizontal reflection plane perpendicular with the principal rotation axis.
• There is NO `C_2` axis perpendicular to the principal axis, making this NOT a dihedral (`D`) group.
• There IS a center of inversion.

Because of this, this should be classified as `bb(C_(2h))`.