Step 1. Write the balanced chemical equation.
The balanced equation is
#"2NaN"_3 → "2Na" + "3N"_2#
Step 2. Strategy
The problem is to convert grams of #"NaN"_3# to moles of #"N"_2# and volume of #"N"_2#.
We can use the flow chart below to help us.
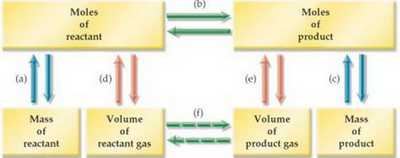
(Adapted from www.lsua.us)
The process is:
(a) Use the molar mass to convert the mass of #"NaN"_3# to moles of #"NaN"_3#.
(b) Use the molar ratio (from the balanced equation) to convert moles of #"NaN"_3# to moles of #"N"_2#.
(e) Use the Ideal Gas Law to convert moles of #"N"_2# to volume of #"N"_2#.
In equation form,
#"grams of NaN"_3 stackrelcolor(blue)("molar mass"color(white)(ml)) (→) "moles of NaN"_3 stackrelcolor(blue)("molar ratio"color(white)(ml))→ "moles of N"_2 stackrelcolor(blue)("Ideal Gas Law"color(white)(ml))(→) "volume of N"_2#
The Calculations
(a) Moles of #"NaN"_3#
#156 color(red)(cancel(color(black)("g NaN"_3))) × ("1 mol NaN"_3)/( 65.01 color(red)(cancel(color(black)("g NaN"_3)))) = "2.40 mol NaN"_3 #
(b) Moles of #"N"_2#
#2.40color(red)(cancel(color(black)("mol NaN"_3))) × ("3 mol N"_2)/(2 color(red)(cancel(color(black)("mol NaN"_3)))) = "3.60 mol N"_2#
(c) Volume of #"N"_2#
The Ideal Gas Law is
#color(blue)(bar(ul(|color(white)(a/a)PV = nRTcolor(white)(a/a)|)))" "#
We can rearrange this to give
#V = (nRT)/P#
#n = "3.60 mol"#
#R = "8.314 Pa·m"^3·"K"^"-1""mol"^"-1"#
#T = "(27 + 273.15) K" = "300.15 K"#
#P = 1.1 × 10^5color(white)(l) "Pa"#
∴ #V = (3.60 color(red)(cancel(color(black)("mol"))) × 8.314 color(red)(cancel(color(black)( "Pa")))·"m"^3·color(red)(cancel(color(black)("K"^"-1""mol"^"-1"))) × 300.15color(red)(cancel(color(black)( "K"))))/(1.1 × 10^5 color(red)(cancel(color(black)("Pa")))) = "0.082 m"^3 = "82 dm"^3#
The volume of #"N"_2# produced is #"82 dm"^3#.


