Question

Question #a5469

Answer 1

Let us look at the experimental setup as shown in the figure below.
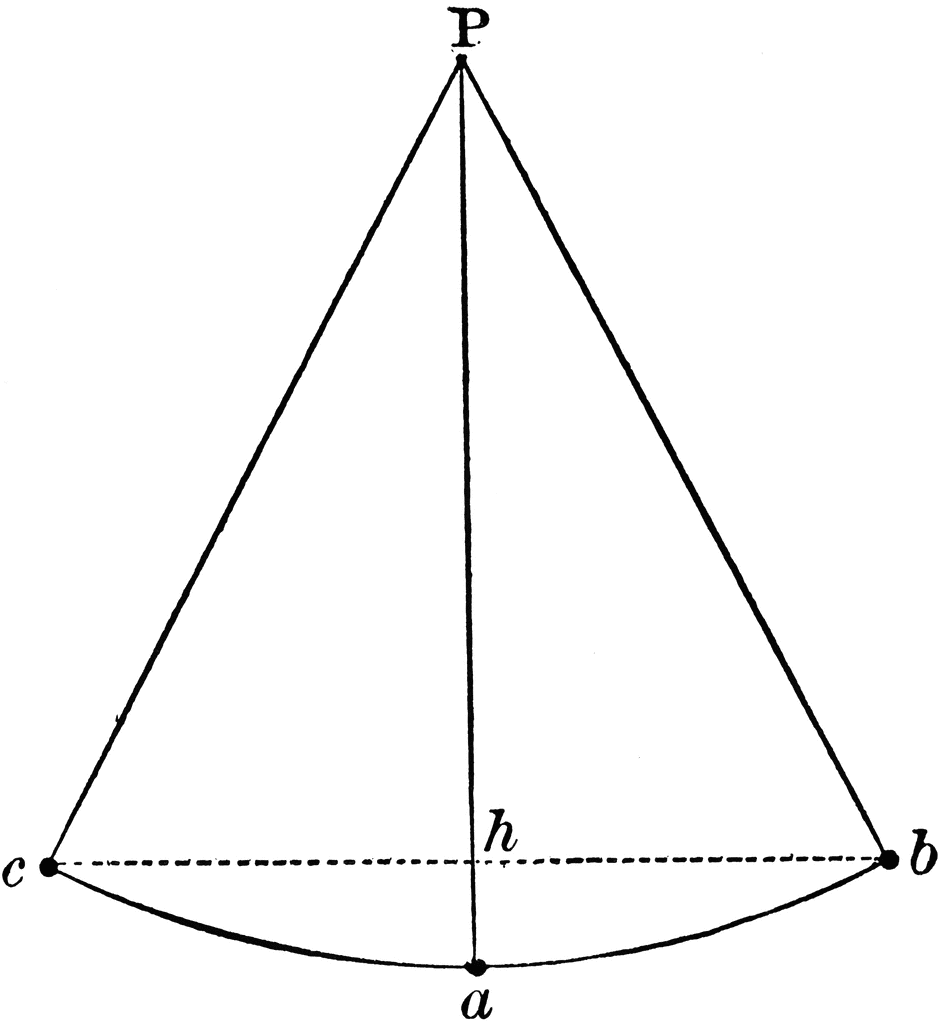
A bowling ball is tied securely to a rope and hung from pivot `P` from the ceiling. Let `mg` be the weight of the ball. The ball be stationary at mean position `a` initially.
Suppose the volunteer stands at point `c`. The ball is pulled to touch the chin of volunteer. Notice that the ball is raised by height `h` as compared to mean position `a`, thereby giving it potential energy`=mgh`.

As the ball is allowed to just let go (without any push or adding energy) it swings towards mean position `a`. The potential energy decreases and gets converted to its kinetic energy as it moves.
At location `a`, where `h=0`, all the potential energy gets converted to its kinetic energy.

It overshoots and continues its swing towards `b`. Now its kinetic energy starts getting converted back in to potential energy. Once it reaches `b` it stops momentarily. At this point it has potential energy`=mgh` and zero kinetic energy.

We note that at any point of time during its swing, the sum of instantaneous potential energy and kinetic energy remains constant`=mgh`. This is Law of Conservation of energy.

Now the ball reverses its journey to `c` through `a`. Once the ball reaches `c`, it will have only original potential energy. As such it will reach up to chin of volunteer (original position) but never hit him.

In real life situation, some energy is always lost due to mechanical friction of the pivot and also due to air friction encountered by the ball. Therefore, the ball may not even be able to reach chin of the volunteer after one swing.