Why are #s# orbitals shaped like spheres but #p# orbitals shaped like dumbbells?
1 Answer
Because the
I'm going to introduce a bit of hard math, but I'll point out the important things. If you have a grasp on some physics and can visualize a little, this should be accessible/approachable.
We can look at example wave functions of the
In general, the wave function is notated like this:
#psi_(ns"/"p"/"etc)(r,theta,phi) = R_(nl)(r)Y_(l)^(m_l)(theta,phi)#
where:
#n# ,#l# , and#m_l# are the principal, angular momentum, and magnetic quantum numbers, respectively, and we are in spherical coordinates (one radial coordinate and two angular coordinates).#R# is a function of#r# , describing how the radius of the orbital changes, and#Y# is a function of#theta# and#phi# , describing how the shape of the orbital changes.
The example wave functions are (
#psi_(1s) = 1/(sqrtpi)(Z/(a_0))^"3/2"e^(-"Zr/a"_0)#
#psi_(2p_z) = 1/(4sqrt(2pi)) (Z/(a_0))^"5/2" re^(-"Zr/2a"_0)costheta# where
#Z# is the atomic number and#a_0 = 5.29177xx10^(-11) "m"# is the Bohr radius.
Basically...
- If you examine
#psi_(1s)# , you can see no dependence on#theta# or#phi# , only#r# . That means it's spherically symmetric. If only#r# is changing, it can only be a sphere, and thus, it has no directionality. - If you look at
#psi_(2p_z)# , you can see a dependence on#r# and a dependence on#theta# (in the#costheta# ). This is what gives the orbital a non-spherical shape.
It's not obvious however, how the
The angular momentum is what reacts to a magnetic field, creating a "precessional orbit" about the
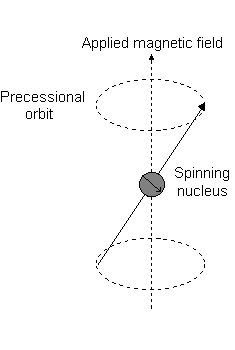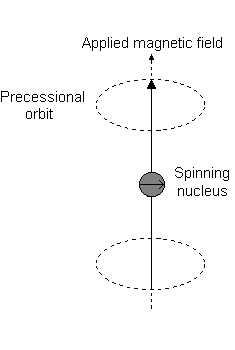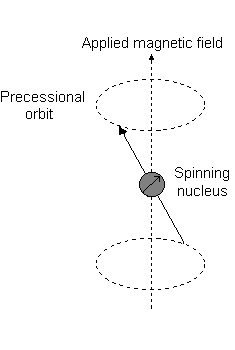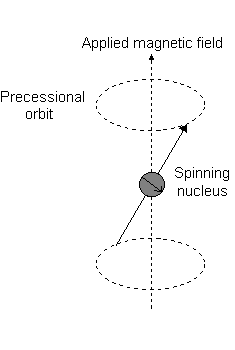
For the angular momentum operator
For
However, for
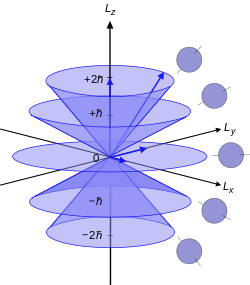
The only difference with this image is that for

