What is degeneracy as opposed to a degenerate state? How can we know what orbitals are higher in energy?
1 Answer
This is a kind of complicated question.
- A degenerate state is a state in which the energy is the same as other states.
- A degeneracy is the number of states that have that same energy, and is described as
2l+1 .
So, the difference is that degeneracy describes how many states, and a degenerate state is specifically which ones count.
- Any
ns orbital is the same energy for the samen . - No,
p andd orbitals of the samen don't necessarily have the same energy (not even in hydrogen atom). - I cannot tell you the energy of every orbital, because their energies change throughout the periodic table, and sometimes the actual ordering is different.
DEGENERATE STATES
Atomic orbitals that share the same principal quantum number
 http://www.chemtube3d.com/
http://www.chemtube3d.com/
(if they share the same
On the other hand, if their
For example, the
- They do not have the same shape (different
l ). - They do not have the same total number of radial nodes (different
n - l - 1 ). - They do not have the same number of angular (planar) nodes (different
l ). - Maybe some combination of all three.
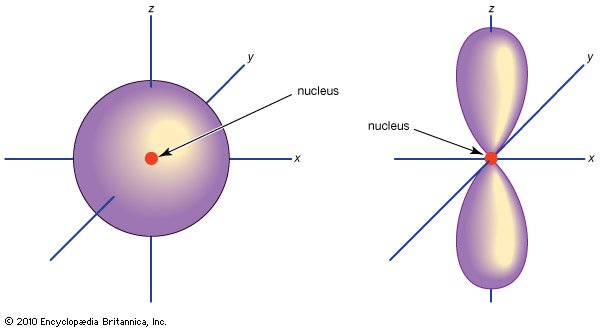 http://media-3.web.britannica.com/
http://media-3.web.britannica.com/
However, the
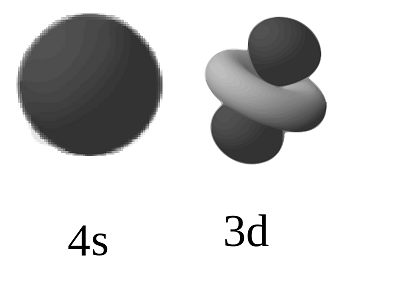 4s and 3d orbitals
4s and 3d orbitals
One might call them degenerate once the energies get close enough. When comparing their
DEGENERACY
Like I said, degeneracy is just the number of orbitals of the same energy. Typically we say, for example:
- The
np atomic orbitals are triply degenerate, because there are three of them in a free atom, and they are all equivalent orbitals with equivalent energies. - The
np atomic orbitals have a degeneracy of2l + 1 = 3 , since theirl is equal to1 .
For example, a
ul(uarr darr) " " ul(uarr color(white)(darr)) " " ul(uarr color(white)(darr))
underbrace(" "" "" "" "" "" "" "" ")
2p_x" "" "2p_y" "" "2p_z

