Question

Show that the sum of the interior angles of a Quadrilateral is 360 degrees?

Answer 1

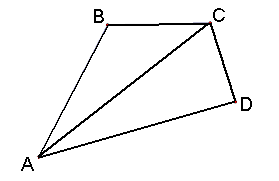
Consider a Quadrilateral `ABCD`. We join `AC`

For the triangle `ABC`:

We know the interior angles add up to `180^o`
`:. angleBAC + angleACB + angleABC = 180^o` ..... [A]

Similarly, for the triangle `ACD`:

`:. angleCAD + angleADC + angleACD = 180^o` ..... [B]

Now:

`angleBAD = angleBAC + angleCAD` ..... [C]
`angleBCD = angleACB + angleACD` ..... [D]

And the sum of the interior angles of the Quadrilateral `ABCD` is:

`S = angleABC + angleBCD + angleCDA + angleBAD`

Using `[C]` and `[D]` this becomes:

`S = angleABC + (angleACB + angleACD) +`
`" " angleADC + (angleBAC + angleCAD)`

`\ \ = (angleBAC + angleACB + angleABC) +`
`" " (angleCAD + angleADC + angleACD)`

and, using `[A]` and `[B]` this becomes:

`S = 180^o + 180^o`
`\ \ = 360^o \ \` QED