Question #59f7b
1 Answer
Jan 2, 2018
See the explanation.
Explanation:
If a function
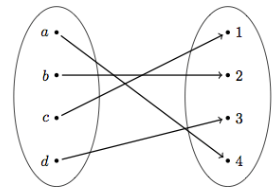
The figure is the example of a bijective function. If you choose one element from the right elipse, you can know the corresponding element in the left oval.
It is a good way to draw a graph of the function if you want to know whether it is bijective.
graph{2x+1 [-5, 5, -5, 5]}
graph{x^2 [-5, 5, -5, 5]}
Then, how about
graph{xtan((pix)/2) [-1, 1, -5, 5]}
The function
For example,
Therefore, it has no inverse.

