Inverse Variation Models
Key Questions
-
Nice question i had some of these questions for my homework so i shall share them with you.
So i will do it in a paint pic.

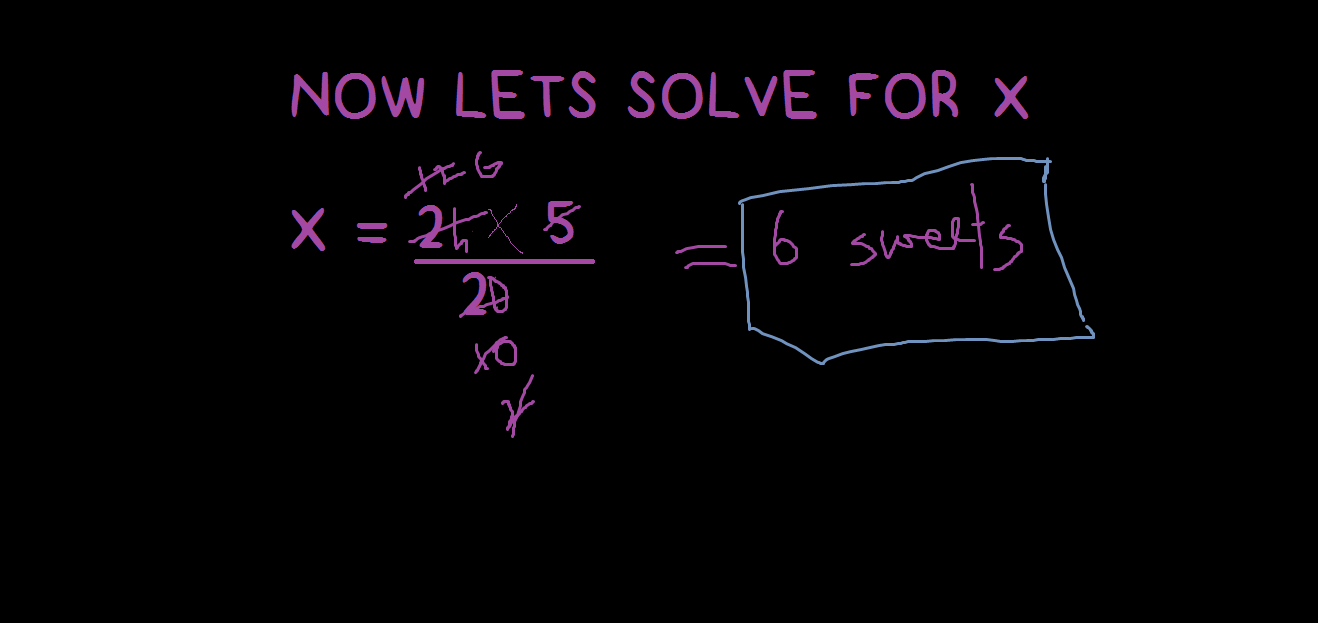
-
Let's say a family husband is working, so if more people works in family, more income for the family. It is an example of direct variation.
If family has less members, more saving (provided that the family has the same amount of income). More members, less saving ( income is still the same). It is an inverse variation.
more members work = more earning in family
more members = less saving in family
More members is in joint variation to earning and saving.
1) Direct variation -- as the independent variable increases so does the dependent variable.
The amount of money a person who is paid hourly makes varies directly with the number of hours worked.
P=kh where P is the pay, h the number of hours, and k, the proportionality constant, is the hourly wage.
2) Inverse variation -- as the independent variable increases, the dependent variable decreases or vice versa.
The worth of a car varies inversely with its age.
#W=k/a where W # is the worth of a car at age a and k is the proportionality constant.3) Joint variation -- the dependent variable varies directly with two or more independent variables.
The gravitational pull between two objects varies jointly with their masses and inversely with the square of the distance between them.
#F=g(m_1m_2)/d^2# where g is the gravitational constant. -
Answer:
see explanation below;
Explanation:
Inverse variation models, is a term used in inverse variation equation..
for example;
#x# varies inversely proportional to#y# #x prop 1/y# #x = k/y# , where#k# is constantthis then means that, when value
#y# increases, value#x# will decrease, since its inversely proportional.For more information about Inverse variation model, this video link would aid you; Inverse Variation Model
Questions
Rational Equations and Functions
-
Inverse Variation Models
-
Graphs of Rational Functions
-
Division of Polynomials
-
Excluded Values for Rational Expressions
-
Multiplication of Rational Expressions
-
Division of Rational Expressions
-
Addition and Subtraction of Rational Expressions
-
Rational Equations Using Proportions
-
Clearing Denominators in Rational Equations
-
Surveys and Samples