Almost line in the #xy# plane can be expressed as #y=mx+b# where #m# is the line's slope and #b# is its #y#-intercept. The exception is when the slope of the line is undefined, that is, in the case of a vertical line.
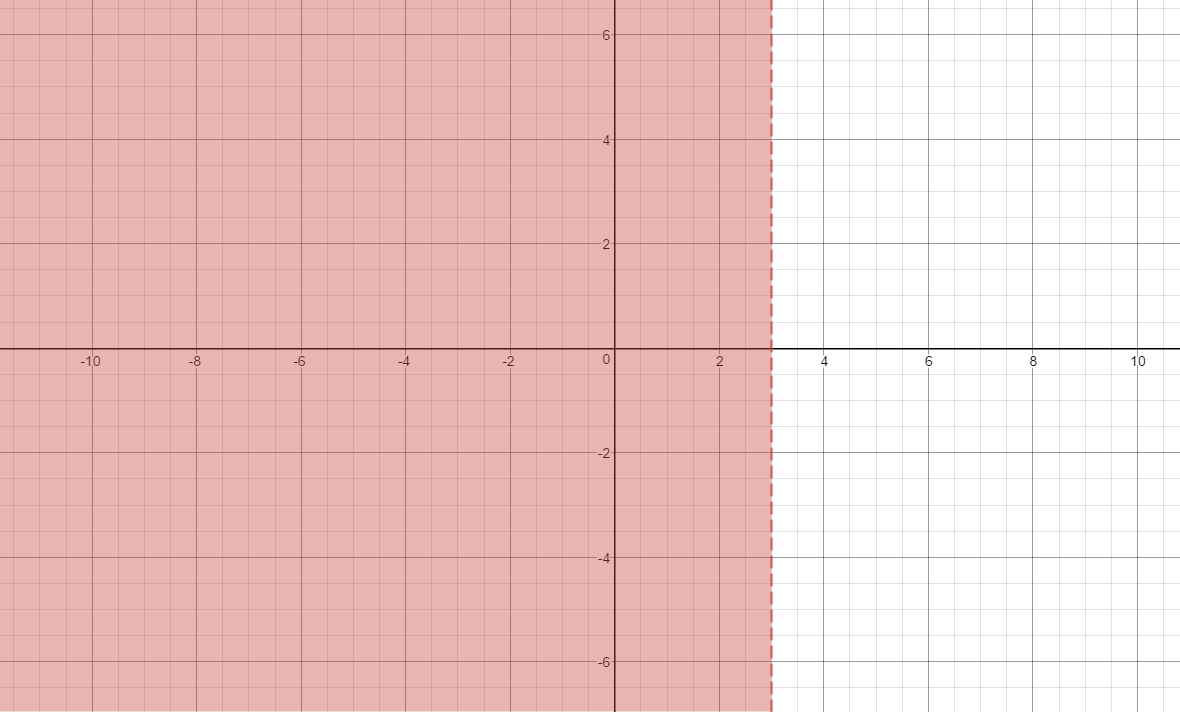
A vertical line has an equation of the form #x=c# for some constant #c#. If an inequality has such a line as a boundary, we simply pick whichever side of that line contains points satisfying the inequality and shade that, just as we would with a line that has a defined slope.
For example, here is the graph of #x<3#:
In a system of inequalities, we just shade as normal for each inequality, and then keep wherever all of the shadings overlap.
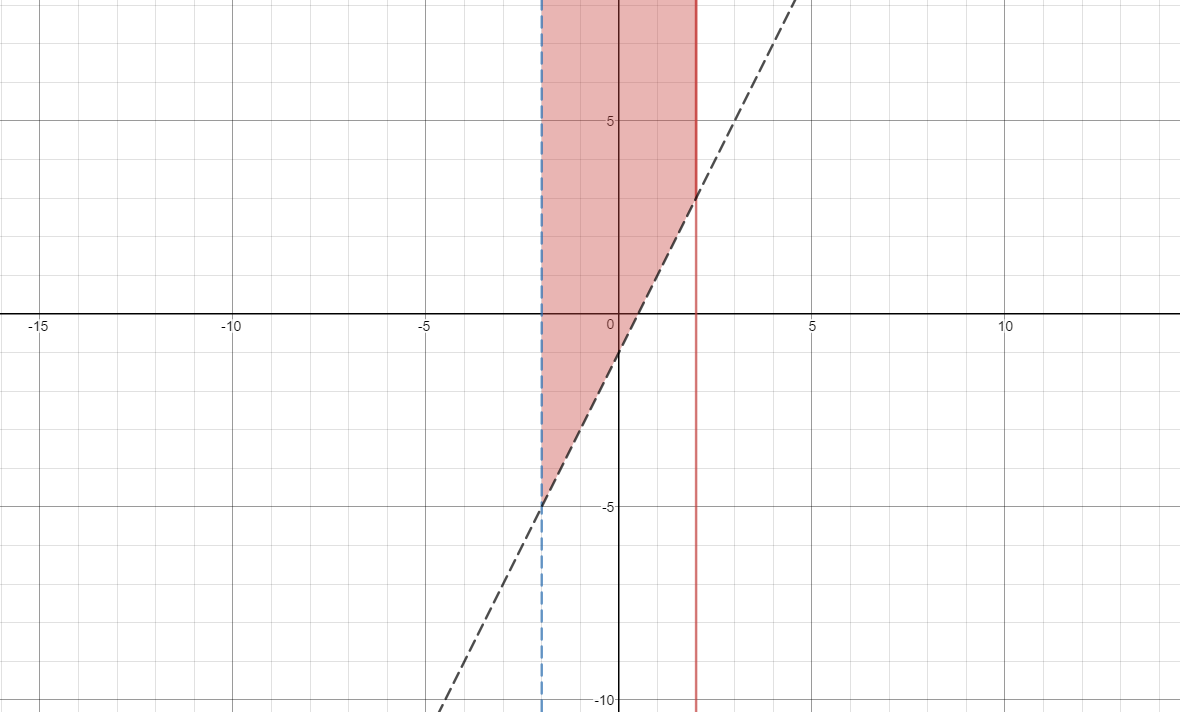
If we have #{(x > -2), (x <= 2), (y > 2x-1):}#
we would graph the three lines generated by equalities (remembering to used dashed lines for #># or #<# and solid for #>=# or #<=#), and then keep the portion in which all three shaded areas overlap, giving us this: