Question

Question #db2b4

Answer 1

The underlying principle of conservation of energy is explained here
For sake of completeness I am reproducing extracts from that answer.

See the pendulum setup as shown in the figure below, same as given fig `(a)`

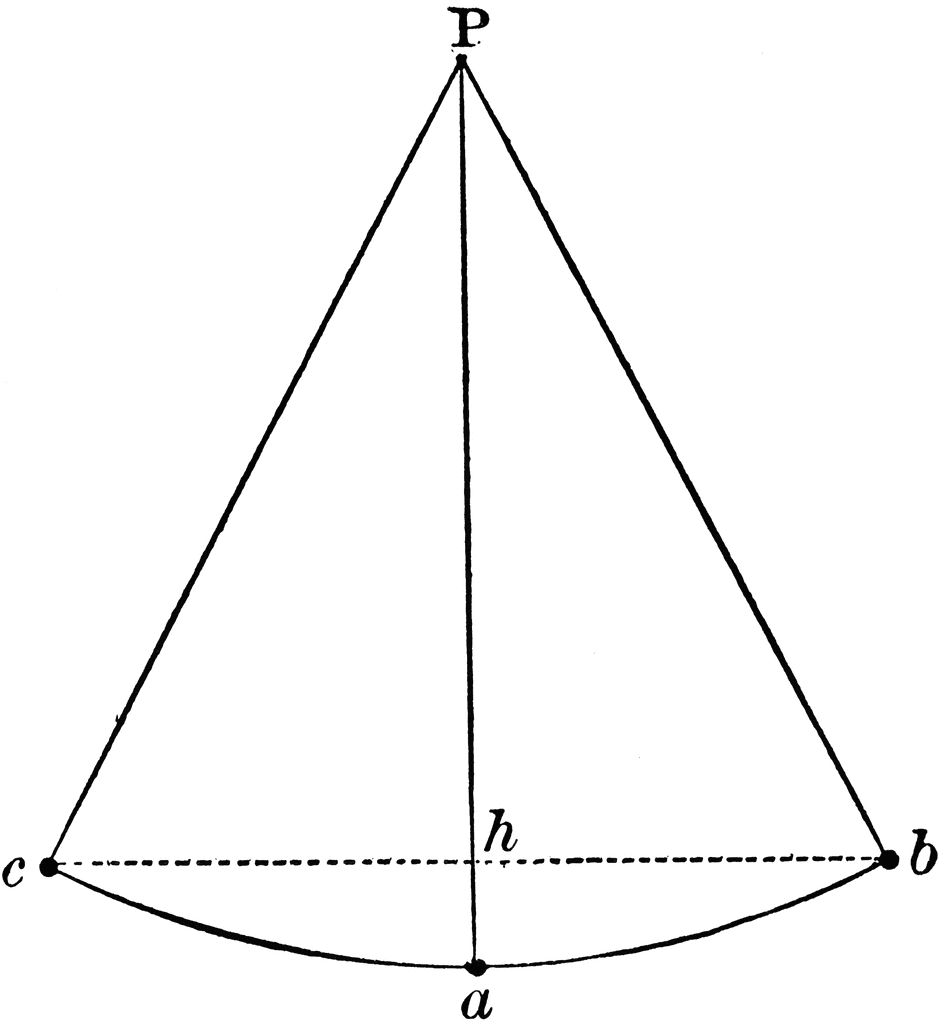
A ball is tied securely to a string and hung from pivot `P` from the ceiling. Let `mg` be the weight of the ball.

During its swings when the ball is at extreme positions `c` or `b`, notice that the ball is raised by height `h` as compared to mean position `a`, thereby giving it potential energy`=mgh`.

Let the ball swings from extreme position `c` towards mean position `a`, the potential energy decreases and gets converted to its kinetic energy as it moves.
At location `a`, where `h=0`, all the potential energy gets converted to its kinetic energy.

It overshoots and continues its swing towards `b`. Now its kinetic energy starts getting converted back in to potential energy. Once it reaches `b` it stops momentarily. At this point it has potential energy`=mgh` and zero kinetic energy, same as at position `c`.

We note that at any point of time during its swing, the sum of instantaneous potential energy and kinetic energy remains constant`=mgh`. This is Law of Conservation of energy.

This discussion clearly indicates that extreme position of the ball will always be at a height `h`, if we ignore frictional forces.

As one can see that any point lying on the dotted line `AB` of given fig `(b)` will be located at height `h`. As such above conclusion is also applicable for any other extreme point including point D.
Needless to say that option (D) can be ruled out due to shortened length of string with new pivot at point C.