What do #n#, #l#, and #m_l# tell us about an orbital?
1 Answer
The quantum numbers
Explanation:
The wave function of an orbital (its probability pattern) is determined by three quantum numbers.
The principal quantum number
The principal quantum number determines the size of an orbital and its probability pattern.
The bigger the principal quantum number the bigger the orbital.

The size of an orbital is roughly proportional to the value of
The azimuthal quantum number,
The azimuthal quantum number determines the shape of an orbital.
If
The probability pattern has the shape of a sphere, as in the above image.
If
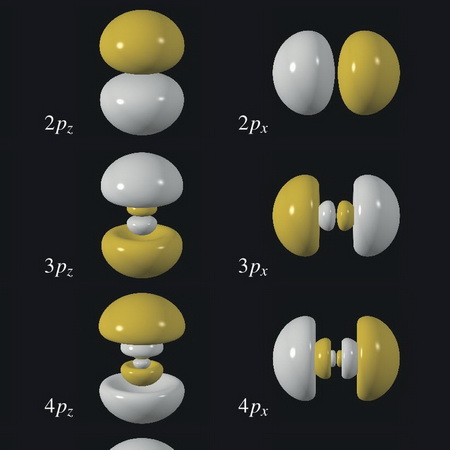
(From WebElements)
The picture does not show the relative sizes of the orbitals, but it does show their general shapes.
The magnetic quantum number
The magnetic orbital determines the number of orbitals of a given type and the directions they point in a magnetic field.
For a
Thus, there are three different
We see the

