Question #65a2a

Question

980 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-04-16T23:33:14

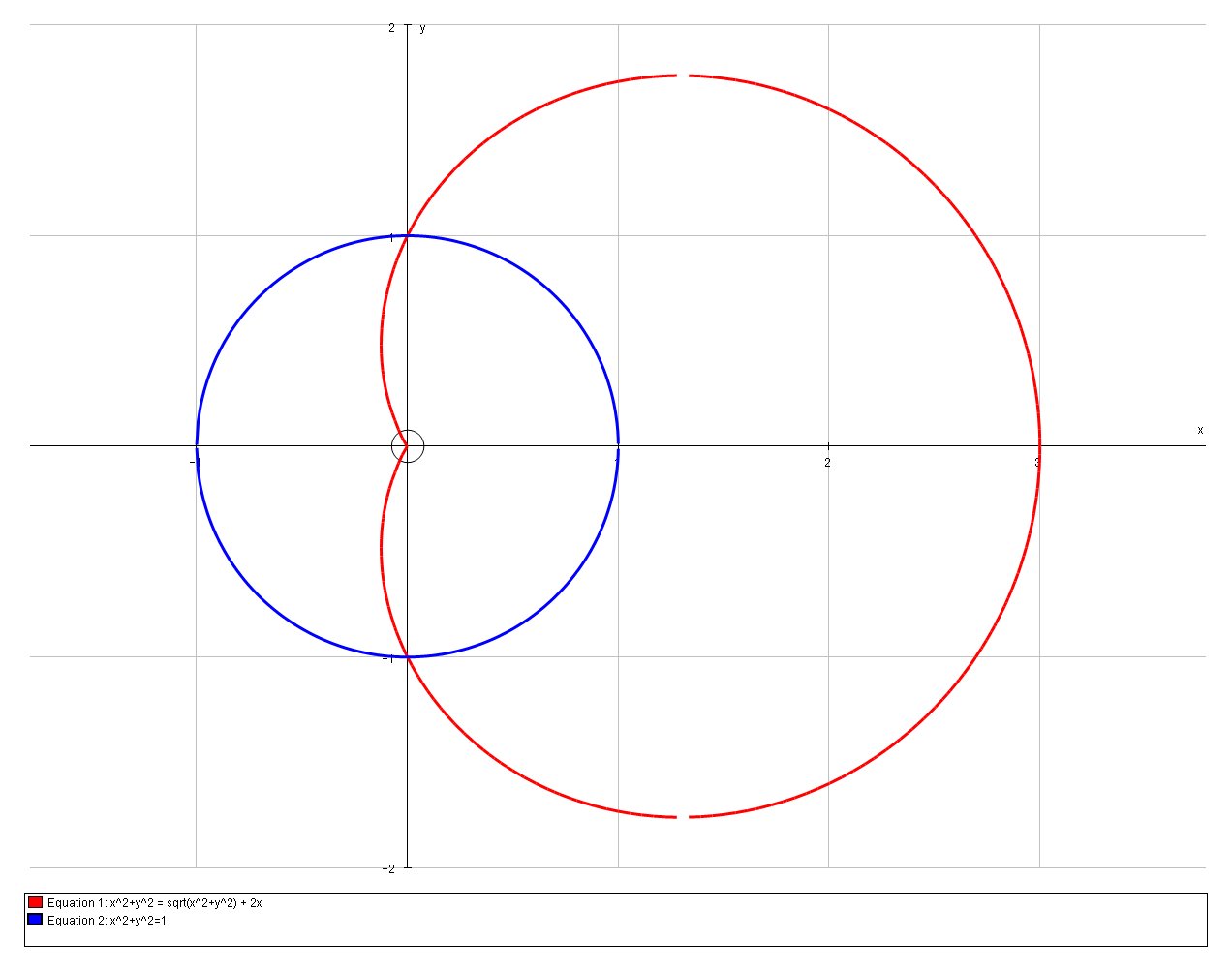
# x^2+y^2 = sqrt(x^2+y^2) + 2x#

intersection coordinates are #(0,-1)# and #(0,1)#

Our Polar equation is:

# r = 1+2cos theta#

To convert from polar to rectangular (Cartesian) coordinates we use the fundamental relationship:

# {: (x = rcos theta), (y = rsin theta) :} \ \ # and # \ \ x^2+y^2 = r^2 #

So we can transform our equation as follows:

# r = 1+2cos theta#
# :. r^2 = r + 2rcos theta#
# :. x^2+y^2 = sqrt(x^2+y^2) + 2x#

For the interaction with a unit circle which would have the equation:

# x^2+y^2 = 1 #

We would have:

# :. 1 = 1 + 2x => 2x =0 #
# " " => x=0#

And:

# x=0 => y^2 = 1 #
# " " => y = +-1 #

So the intersection coordinates would be #(0,-1)# and #(0,1)#

enter image source here