Question

What is the molecular electron configuration of `"O"_2`?

Answer 1

`(sigma_(1s))^2(sigma_(1s)^"*")^2(sigma_(2s))^2(sigma_(2s)^"*")^2(sigma_(2p_z))^2 (pi_(2p_x))^2(pi_(2p_y))^2(pi_(2p_x)^"*")^1(pi_(2p_y)^"*")^1`

You should read the explanation on how we came up with this, below.

---

When determining the molecular orbital (MO) configuration of a homonuclear diatomic molecule like `"O"_2` or `"F"_2`, first, we should determine the atomic orbital (AO) configuration.

We had for each `"O"`:

`1s^2 2s^2 2p^4`

The AOs of `"O"` are therefore the `1s`, `2s`, and `3xx2p` orbitals.

LINEAR COMBINATION OF ATOMIC ORBITALS

The number of AOs in equals the number of MOs out.

Any `ns` orbitals combine together head-on:

• In-phase to form `sigma_(ns)`/sigma bonding MOs
• Out-of-phase to form `sigma_(ns)^"*"` antibonding MOs

The `1s` and `2s` overlap in the same way:

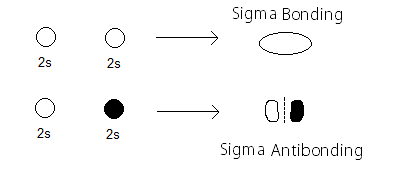
with a partial MO diagram like this:

Along the internuclear (`z`) axis, the `np_z` AOs combine head-on in a similar manner:

• In-phase to form `sigma_(np_z)` bonding MOs
• Out-of-phase to form `sigma_(np_z)^"*"` antibonding MOs

Here's how the `2p_z` overlap:

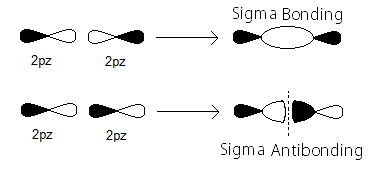
The partial MO diagram depiction of those is similar to the `ns` overlap, just a wider energy gap, and collectively higher in energy.

Finally, the `2p_x` and `2p_y` combine sidelong/sideways, so that they make `pi_(2p_x)` and `pi_(2p_y)` bonding, and `pi_(2px)^"*"` and `pi_(2p_y)^"*"` antibonding MOs instead:

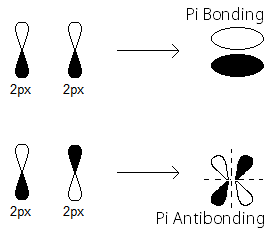
For homonuclear diatomics after `"N"_2`, the energy ordering is like this for these six MOs:

This portion of the MO diagram (the `2p` overlaps) are significantly higher in energy, because the AOs started off at a significantly higher energy.

Overall, the MO diagram is therefore like this:

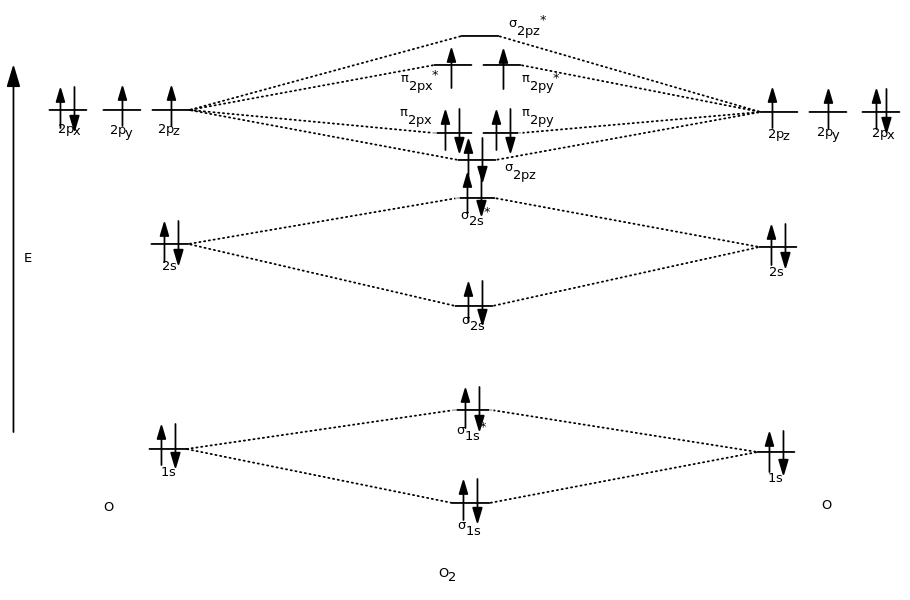
The MOs were filled just like the AOs would be filled according to the Aufbau Principle, Hund's Rule, and the Pauli Exclusion Principle.

So, write the MO configuration based on this diagram. Start with the lowest-energy orbital, and indicate the electrons in each kind of orbital, just like atomic electron configurations.

You should get:

`color(blue)((sigma_(1s))^2(sigma_(1s)^"*")^2(sigma_(2s))^2(sigma_(2s)^"*")^2(sigma_(2p_z))^2 (pi_(2p_x))^2(pi_(2p_y))^2(pi_(2p_x)^"*")^1(pi_(2p_y)^"*")^1)`