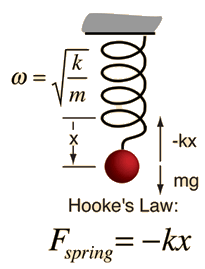
Let us consider that a sphere of mass #m# is hanged through spring of negligible mass from a support and the spring posseses spring constant #k#
If the spring is elongated by length #x# from its equilibrium position, then by Hooke's law the force exerted by the spring will be given by
#F_"spring"=-kx......[1]#
Now if the mass m executes SHM of ampltude #A# here then displacement #x# of mass #m# from equilibrium position will be related with time as follows
#x=Asin(omegat)......[2]#, where #omega# represents the angular velocity of refference point associated with the SHM.
Differentiating equation [2] w.r to t we get velocity #v#
#v=(dx)/(dt)=Aomegacos(omegat)=Awsqrt(1-sin^2(omegat))#
#=>v=omegasqrt(A^2-x^2)....
[3]#
Differentiating [2] twice w.r to t we get acceleration (#a#) on mass #m#
#a=(d^2x)/(dt^2)=-Aomega^2sin(omegat)=-omega^2x....[4]#
So by Newtons law the restoring force on mass m when its displacement is #x#, will be given by
#ma=-momega^2x......[5]#
This force should be same as that obtained by Hooke's law earlier. So comparing [1] and [5] we get
#F_"spring"=-kx=ma=-omega^2x#
#=>omega^2=k/m#
#=>omega=sqrt(k/m)....[6]#
By equation [4] the maximum acceleration of the mass will be when #x=A#
So #a_"max"=omega^2A=k/mxxA#
Inserting #m=200g=0.2kg#
#k=400N/m# and #A=10cm=0.1m#
we get #a_"max"=400/0.2xx0.1=200"m/"s^2#
Putting #x=0# in [3] we get maximum velocity
#v_"max"=Aomega=Axxsqrt(k/m)#
#=0.1xxsqrt(400/0.2)"m/s"=sqrt20"m/s"#


