Question #89bdd
1 Answer
Jan 21, 2017
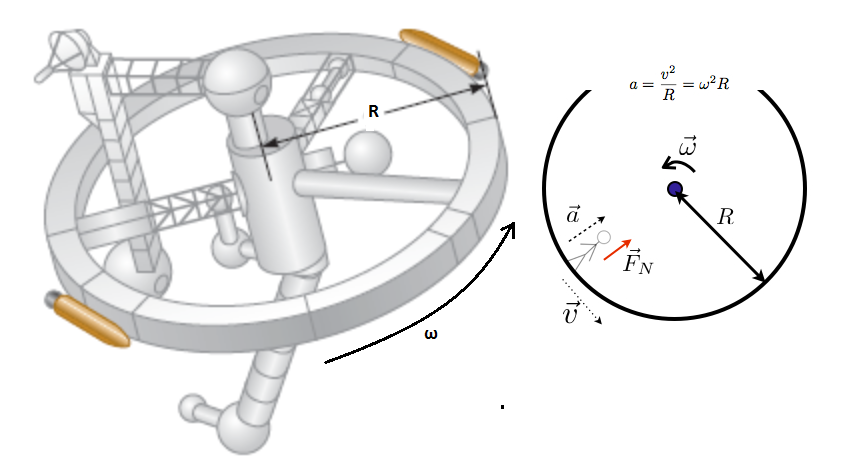
Here it is given that the space station is spinning with an angular speed (
So
So centripetal acceleration produced
So

Here it is given that the space station is spinning with an angular speed (
So
So centripetal acceleration produced
So