At constant volume in a closed container, how do you explain that increasing temperature leads to increasing gas pressure?
1 Answer
There are two ways to explain it.
Here's the context.
At a constant volume, we have a rigid container. We can keep the quantity of gas constant simply by making sure the container is sealed tight.
Overall, we have a rigid, closed container.
CONCEPTUAL WAY
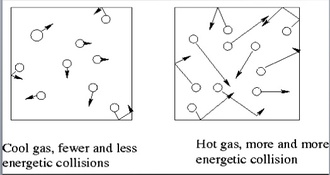
Heating the gas inside will make the gas particles move faster, and they will collide with the walls more often.
Pressure is defined as the force per unit area:
#P = F/A#
So, the higher the temperature, the higher the speed in general for each gas particle, and the stronger the force at which it hits the walls of the container.
Therefore, the pressure is higher.
MATHEMATICAL WAY
From the ideal gas law:
#PV = nRT#
Keeping volume and mols of gas constant, we have the initial and final states as:
#P_1V = nRT_1#
#P_2V = nRT_2#
Dividing these equations, we get:
#P_2/P_1cancel((V/V)) = cancel(((nR)/(nR))) T_2/T_1#
#=> P_2/T_2 = P_1/T_1 = "const"#
If the temperature is increased,
If
Therefore,

