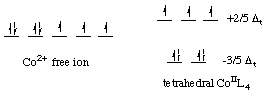Question

What kinds of electron configurations can we get with octahedral and tetrahedral `"Co"^(2+)` complexes?

Answer 1

WARNING! Long answer! The octahedral complexes are either `t_text(2g)^6 color(white)(l)e_text(g)` (low-spin) or `t_text(2g)^4color(white)(l) e_text(g)^3` (high-spin).

Explanation:

Almost all the tetrahedral complexes are `e_text(g)^4color(white)(l) t_text(2g)^3` (high-spin).

Crystal Field Theory

In an octahedral field, the the five degenerate `"d"` orbitals are split into two groups:

• two high-energy orbitals, designated as `e_g`
• three low energy orbitals, designated as `t_2g`.

The difference between the energy levels is `Δ_text(o)`.

The value of `Δ_text(o)` depends on both the metal and the nature of the ligands.

In a tetrahedral field, the energy levels are reversed.

The `"d"` orbitals split into:

• three `t_2g` high-energy orbitals
• two `e_g` low-energy orbitals

Octahedral `"Co"^"2+"` complexes

The electron configuration of `"Co"^"2+""` is `"[Ar]3d"^7`.

When we have a strong-field ligand like `"CN"^"-"`, `Δ_text(o)` is relatively large.

The extra electrons occupy the lower `t_(2g)` set of orbitals before they go into the upper `e_g` levels.

(Adapted from chemed.chem.purdue.edu)

When we have a weak-field ligand like `"H"_2"O"`, `Δ_text(o)` is relatively small.

The electrons fill the orbitals in a Hund's Rule type of order and pair up only when they have no other choice.

`["Co"("H"_2"O")_6]^"2+"` has the maximum number of half-filled orbitals and is called a high-spin state.

A high-field ligand like `"CN"^"-"` causes `Δ_text(o)` to be so large that the lower orbitals are filled in before the higher orbitals.

Thus, `["Co"("CN")_6]^"4-"` has a filled set of low-energy orbitals and is called a low-spin state.

Tetrahedral `"Co"^"2+"` complexes

`Δ_text(t)` is about half the size of `Δ_text(o)`, so almost all tetrahedral complexes are weak field/high spin.

Thus, tetrahedral `"Co"^"2+"` complexes have an `e_text(g)^4color(white)(l)t_text(2g)^3` configuration.