Show that #CM# and #RQ# are perpendicular ?
2 Answers
See below.
Explanation:
Given
The circle's center is
so
Finally
Attached a figure
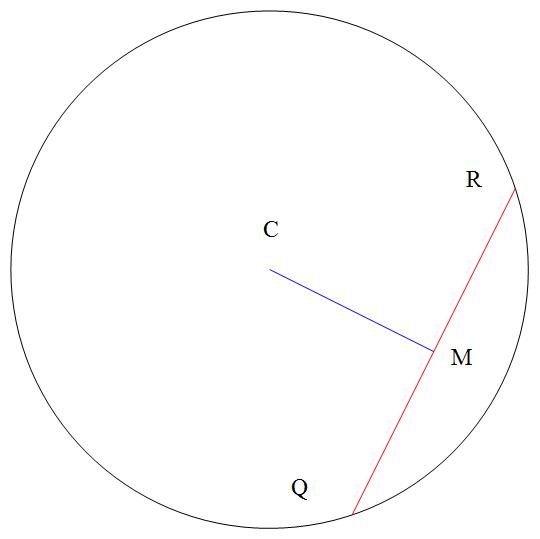
The x coordinate of the chord goes from
The y coordinate of the chord goes from
The coordinates of the midpoint are
The slope,
The equation of the circle
The slope,
Please observe that:
This shows that the two lines are perpendicular.

