Question

Question #d93d2

Answer 1

Same charge

Explanation:

For a parallel plate capacitor, its capacitance `C` is given by the expression

`C = ε cdot A /d`
where `A` is the area of one conducting plate, `epsilon and d` are permittivity and thickness of the dielectric.

It is not surprising that the expression for `C` is independent of the material of plates.
Other expression is `C=Q/V_C`, where `Q` is stored charge and `V_C` is applied voltage.

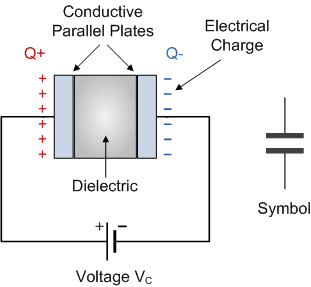
This how the capacitor works:
When we connect the capacitor to a battery, some of the electrons are pulled away from one plate. An equal number of electrons are be pushed on to the other plate. As such one plate has a net negative charge, whereas the other has an equal net positive charge. This results in a difference in electrical potential between the plates, and an electric field exists between the plates.
As long as the battery stays connected across the plates of the capacitor, this electric field is balanced by emf of the battery.

Once the battery is removed, and the circuit is left open, the charges stay on respective plates as these can't move. Thus electric energy is stored in the capacitor in the form of electric charge imbalance and the electric field between the plates.

From the foregoing it is clear that both conducting plates have same charge imbalance irrespective of the material these are made of.