Find the roots of z^5+1=0z5+1=0?
2 Answers
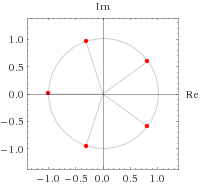
Working to 3dp there are 5 solutions:
z = -1; -0.309+-0.951; z = 0.809+-0.588i z=−1;−0.309±0.951;z=0.809±0.588i
Explanation:
Let
And we will put the complex number into polar form (visually):
|omega| = 1 |ω|=1
arg(omega) = pi arg(ω)=π
So then in polar form we have:
omega = cos(pi) + isin(pi) ω=cos(π)+isin(π)
We now want to solve the equation
z^5 = cos(pi) + isin(pi) z5=cos(π)+isin(π)
Whenever dealing with complex variable equation such as this it is essential to remember that the complex exponential (and therefore the polar representation) has a period of
z^5 = cos(pi+2npi) + isin(pi+2npi) \ \ \ n in ZZ
By De Moivre's Theorem we can write this as:
z = (cos(pi+2npi) + isin(pi+2npi))^(1/5)
\ \ = cos((pi+2npi)/5) + isin((pi+2npi)/5)
\ \ = cos theta + isin theta \ \ \ \ wheretheta=((2n+1)pi)/5
Working to 3dp we get:
Put:
n=-2 => theta = -(3pi)/5
" " :. z = cos (-(3pi)/5)+ isin (-(3pi)/5)
" " :. z = -0.309-0.951i
n=-1 => theta = -pi/5
" " :. z = cos (-pi/5)+ isin (-pi/5)
" " :. z = 0.809-0.588i
n=0 => theta = (pi)/5
" " :. z = cos (pi/5)+ isin (pi/5)
" " :. z = 0.809+0.588i
n=1 => theta = (3pi)/5
" " :. z = cos ((3pi)/5)+ isin ((3pi)/5)
" " :. z = -0.309+0.951
n=2 => theta = pi
" " :. z = cos pi+ isin pi
" " :. z = -1
After which the pattern continues.
We can plot these solutions on the Argand Diagram
Explanation:
If we express
so:
We have then:
for any
We have potentially infinite solutions:
but we can see that if
so that:
In conclusion we have five different solutions for
All this points have module equal to