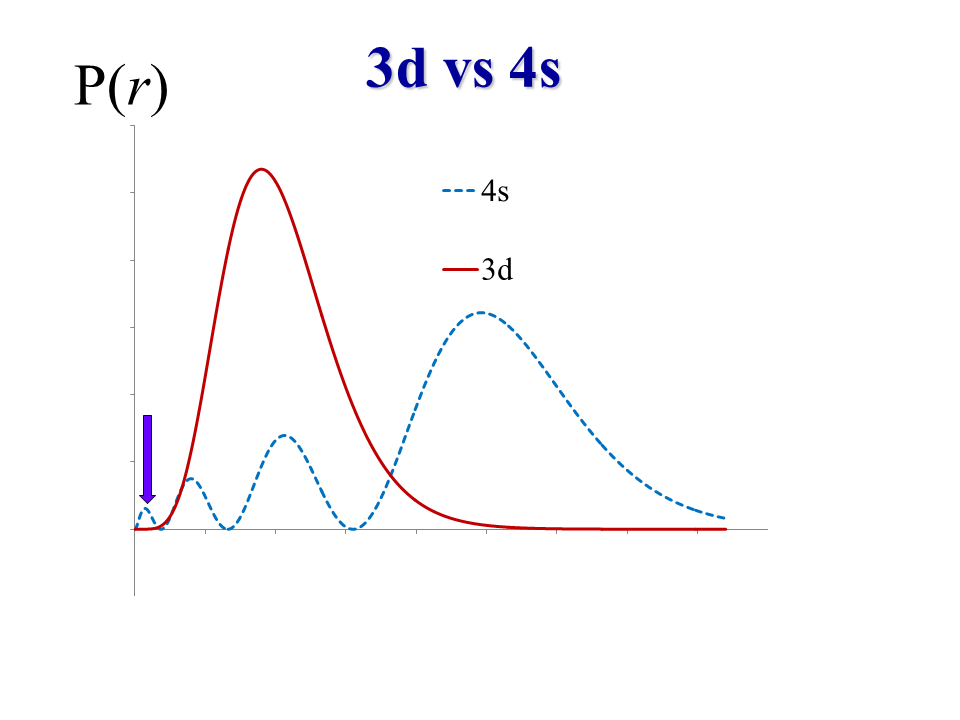
Copper has the electron configuration #[Ar]4s^1 3d^10#. Here is the radial density distribution for the #3d# vs #4s# orbitals, a graph of #4pir^2R_(nl)^2(vecr)# vs. #vecr# (#y# vs. #x#):
(where #R_(nl)(vecr)# is the radial component of the wave function #psi(vecr,theta,phi) = R_(nl)(vecr)Y_(l)^(m_l)(theta,phi)#.)
It tends to be that transition metals, particularly the first-period transition metals (#"Sc","Ti", . . . , "Zn"#) lose their #4s# electrons first because they are farther away from the nucleus on average.
We can tell because the most probable location of the #4s# electron is farther to the right-hand side of the graph than the most probable location of the #3d# electron.
Therefore, the #4s# electron comes off first, and then the second electron removed is the tenth #3d#. This gives:
#[Ar]4s^0 3d^9#
The two electrons removed were therefore:
- #4s# #-># #(n,l,m_l,m_s) = (4,0,0,+1/2)#
- #3d# #-># #(n,l,m_l,m_s) = (3,2,{-2,-1,0,+1,+2},pm1/2)#
where by our convention, we chose #m_s = +1/2# arbitrarily for the one #4s# electron.
For the #3d# electron, we probably could not know whether it was #m_s = +1/2# or #-1/2#.
(Although by Hund's rule, we maintain parallel spins to maximize the spin multiplicity [i.e. keep all the electrons for a given #l# the same spin, usually spin-up by convention], we could just as well have removed the "wrong" [spin-up] electron instead of the spin-down electron and ended up with the remaining electron spin-flipped to be spin-up.)
We do not, however, care about which specific #3d# orbital it came from. It could have been anywhere in the set #m_l = {-2,1,0,+1,+2}#, and we cannot be truly sure which orbital it "came from".

