Question

Question #9f75a

Answer 1

About `1.0144`. Actually, it's more like `1.0137`.

---

The rather annoying hurdle is that a `"psig"` is a unit of pressure defined relative to the atmospheric pressure at sea level... or `"14.696 psi"` (`"1 atm"`).

So, `"1500 psig"` in more common units is...

`"1500 psig" + "14.6959 psi" = "1514.1 psia"`, absolute pounds per square inch, relative to vacuum

`=> "1514.1 psia" xx "1 atm"/"14.6959 psi" = "103.07 atm"`

And of course,

`255^@ "C" + 273.15 = "528.15 K"`.

Methane might as well be a liquid at this point... Actually, it might be a supercritical fluid...

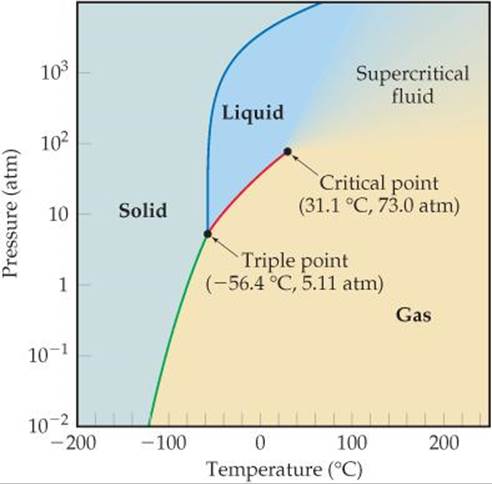
Regardless, the compressibility factor `Z` is defined as:

`Z = (PV)/(nRT)`,

regardless of whether the gas is ideal or not. (It is the true value of `V/n` compared to that of an ideal gas that tells you whether the gas is ideal or not.)

But since we are not told the density of methane, we can only look it up. This is clearly nonstandard pressure, so we would be foolish to use `"22.414 L/mol"` as the molar volume.

Using this calculator for the density of methane, we have that:

`D_(CH_4) = "37.612 g/L"`
(NOT `"0.716 g/L"`!)

Thus, using its molar mass:

`V/n = "1 L"/(37.612 cancel("g CH"_4)) xx (16.0426 cancel("g CH"_4))/"1 mol CH"_4`

`=` `"0.4265 L/mol"`

And so, the compressibility factor would apparently be:

`color(blue)(Z) = (("103.07 atm")("0.4265 L"))/(("1 mol")("0.082057 L"cdot"atm/mol"cdot"K")("528.15 K"))`

`~~ color(blue)(1.0144)`

From the same website as before, the reference value is `1.0137`, so we weren't too far off!