It's likely because the #6s# orbital penetrates more than the #4f# orbital (is closer to the nucleus), which somewhat blocks it from relaxing electrons down into a valid destination orbital. I don't think it's impossible to radiate... but it might be hard.
Well... for instance, platinum is an example of an element with a #4f# orbital. It is the lanthanides that are the first elements in the periodic table to use #4f# orbitals (and platinum is past the lanthanides).

Let's think about what it means to radiate... it means an electron that was previously excited into the #4f# orbital is anticipated to relax down to a lower energy level.
A lower energy level tends to be of a lower principal quantum number #n#, and for simplicity, must be (per the selection rules) different by exactly one integer step of the angular momentum quantum number #l# if one electron moves:
#DeltaL = sum_i l_f - sum_i l_i = pm1#
#DeltaS = sum_i m_(s,f) - sum_i m_(s_i) = 0#
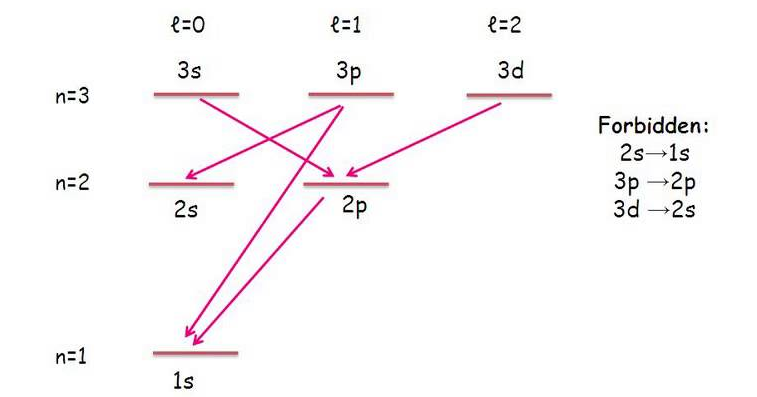
In simpler terms, only diagonal transitions into adjacent orbital columns are allowed.
So, the #4f# would only be expected to be allowed to radiate down to the #ul(4d)# or #ul(3d)# orbitals (no #p# orbitals and no #s# orbitals can take this radiating electron).
The problem is, the #3d# and #4d# are supposed to be nearer the nucleus, and the #4f# is outer-core. Consider the radial density distributions here, which show the electron density of these orbitals:
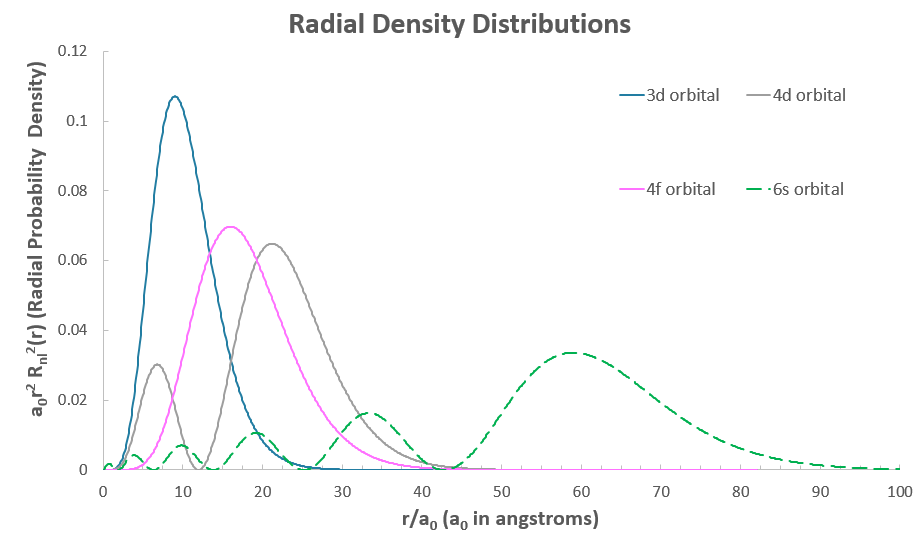
The most probable locations of the electron in the #4d# and #6s# orbitals are farther outside the atom than the #4f#, so we might expect the #4f# electron to relax down into the #3d# orbital.
In a heavy element like platinum, there are significant scalar relativistic effects that lead to the #6s# orbital being contracted, since its electrons approach the speed of light.
That means the #6s# electron(s) penetrate the atom down into the nucleus (seen where the #6s# graph reaches down into the core of the atom, near #r = 0#), while the #4f# orbital has a hard time...
and I would expect that that makes it difficult to radiate the #4f# electron(s) into a valid lower energy level---because the #6s# electron(s) repel them away.

