How many #d# orbitals are there?
1 Answer
Aug 3, 2017
Well, that is given by
Take the
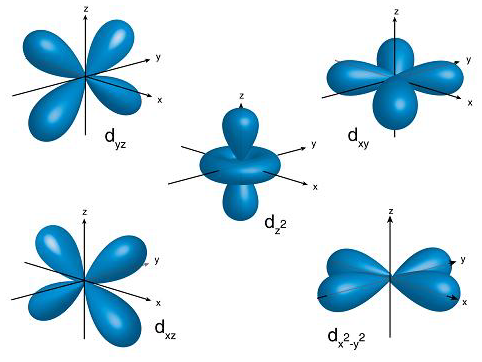
And as such, their magnetic quantum numbers are in the set
#m_l = {-l, -l+1, 0, l-1, l}#
#= {-2, -1, 0, +1, +2}#
And you can see that there are
In the absence of an external field, what is the degeneracy of

