Why is #"Co"("CN")_5^(2-)# paramagnetic?
1 Answer
Well, the first thing you should do is find out the oxidation state of cobalt in this complex ion, so you can find its d-electron count.
From there, by knowing the electron configuration of cobalt in the complex, one can deduce if any of the electrons are unpaired in the complex's molecular orbital diagram.
(We'll work in the realm of crystal field theory and only look at the crystal field splitting diagram that came from the metal's original
If there are any unpaired electrons, we should expect
DISCLAIMER: LONG ANSWER!
FINDING THE OXIDATION STATE OF COBALT
Since cyanide,
#(?) + 5 xx overbrace((-1))^("CN"^(-)) = overbrace(-2)^("overall charge")#
Thus, cobalt is in its
D-ELECTRON COUNT AND COMPLEX'S GEOMETRY
The electron configuration of neutral cobalt is
#[Ar] 3d^7 4s^2# ,
so the electron configuration for
#ul([Ar] 3d^6 4s^0)# ,
and we denote complex as containing a
#underbrace(ul(uarr darr)" "ul(uarr color(white)(darr))" "ul(uarr color(white)(darr))" "ul(uarr color(white)(darr))" "ul(uarr color(white)(darr)))_("3d")#
But this is a complex, and cobalt here has a coordination number of
I won't go too much into the molecular orbital diagram other than the portion of it that comes out of Crystal Field Theory.
CRYSTAL FIELD THEORY (BRIEF REVIEW)
Here, we treat the
- The
#d_(z^2)# is directly along the#z# axis, and is highly destabilized by interacting directly with the metal#d# orbital. - The
#d_(xy)# and#d_(x^2 - y^2)# are somewhat stabilized by their attraction to the positive metal center. - The
#d_(xz)# and#d_(yz)# are about equally stabilized amongst each other, but more stabilized than the#d_(xy)# and#d_(x^2-y^2)# , as the best the ligands can do is line up with their nodal planes.
The crystal field splitting diagram then looks like this:
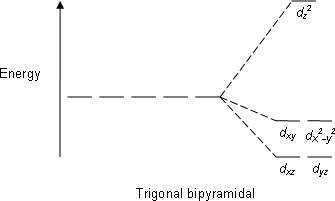
Here we see that the energy gap between
In the end, for this particular geometry, it doesn't matter whether you assume the bottom four
With six
#ul(color(white)(uarr darr)#
#d_(z^2)#
#" "#
#" "#
#" "#
#" "#
#" "#
#" "#
#color(blue)(ul(uarr color(white)(darr))" "ul(uarr color(white)(darr)))#
#d_(xy)" "" "d_(x^2-y^2)#
#ul(uarr darr)" "ul(uarr darr)#
#d_(xz)" "" "d_(yz)#

