Question

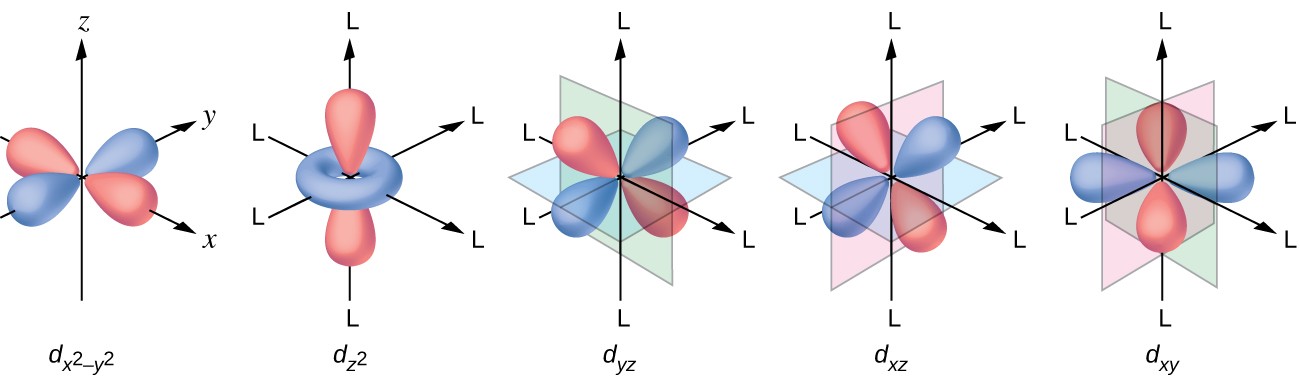
How many orbitals are found in a d subshell?

Answer 1

`5`.

Explanation:

The number of orbitals present in a given subshell is given by the number of values that the magnetic quantum number, `m_l`, can take.

In turn, the possible values that the magnetic quantum number can take depend on the identity of the angular momentum quantum number, `l`, which denotes the energy subshell in which an electron resides in an atom.

`m_l = { -l, -(l-1), ..., - 1, 0, +1, ..., +(l-1), +l}`

Now, the `d` subshell is described by

`l = 2`

This means that for a `d` subshell , the magnetic quantum number can take `5` possible values.

`l = 2 implies m_l = {-2, -1, 0, +1, +2}`

You can thus say that the `d` subshells, which can be found in an atom starting with the third energy level, contain five `d` orbitals.