800. mL of solution has a concentration of 3.0 M. How much water needs to be added to dilute the solution to 1.9 M?
1 Answer
Explanation:
As you know, a dilution is used to decrease the concentration of a given solution.
In order to dilute a given solution, you must make sure that you keep the number of moles of solute present constant and that you increase the total volume of the solution, usually by adding more solvent.
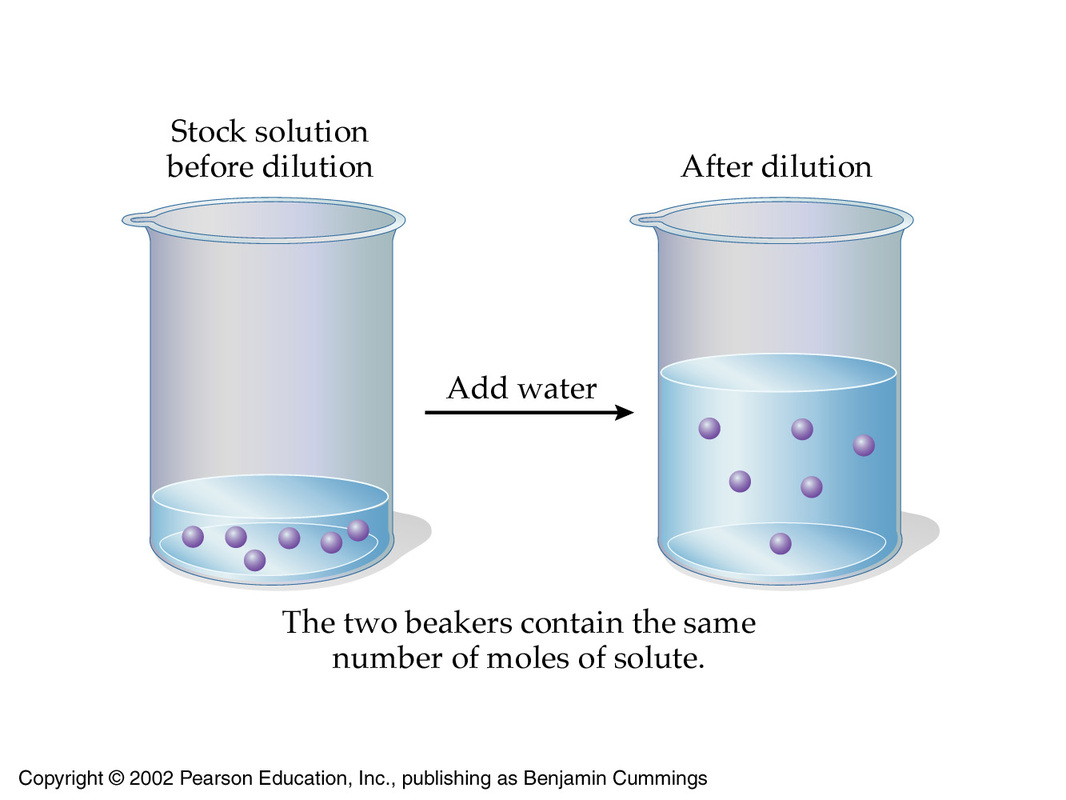
Since molarity is calculated by taking the number of moles of solute present per liter of solution, increasing the volume while keeping the number of moles of solute constant will result in a decrease in concentration.
Mathematically, dilution calculations can be performed using the following equation
The equation for dilution calculations looks like this
#color(blue)(overbrace(c_1 xx V_1)^(color(red)("moles of solute in concentrated solution")) = overbrace(c_2 xx V_2)^(color(red)("moles of solute in diluted solution"))#
Here
Now, you can rearrange this equation to find
#c_1V_1 = c_2V_2 implies c_1/c_2 = V_2/V_1#
This gives you the solution's dilution factor,
#color(blue)(|bar(ul(color(white)(a/a)"D.F." = c_1/c_2 = V_2/V_1color(white)(a/a)|)))#
In your case, the concentration of the solution decreases from
#"D.F." = (3.0 color(red)(cancel(color(black)("M"))))/(1.9color(red)(cancel(color(black)("M")))) = 1.58#
So, if the stock solution was
#"D.F." = V_2/V_1 implies color(purple)(|bar(ul(color(white)(a/a)color(black)(V_2 = "D.F." xx V_1)color(white)(a/a)|)))#
Therefore, the total volume of the diluted solution must be equal to
#V_2 = 1.58 * "800. mL" = "1264 mL"#
The volume of water needed will thus be
#V_2 = V_1 + V_"water"#
#V_"water" = "1264 mL" - "800. mL" = "464 mL"#
I'll leave the answer rounded to three sig figs, despite the fact that you only have two sig figs for the concentration of the two solutions
#V_"water" = color(green)(|bar(ul(color(white)(a/a)"464 mL"color(white)(a/a)|)))#

