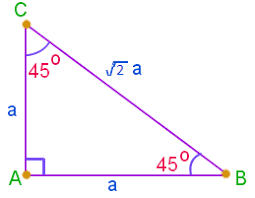
A 45-45-90 triangle has a hypotenuse of length 7. What is the length of one of its legs?

Question

27491 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-05-11T07:38:56

#(7sqrt2)/2#

In a #45-45-90# triangle the two shorter sides are equal since it is also an isosceles triangle. Using Pythagoras' theorem

#x^2+x^2=7^2#

#2x^2=49#

#x=sqrt(49/2#

#x=7/sqrt2=(7sqrt2)/2#

Answer 2 · 2018-05-11T07:46:37

#color(indigo)("Length of each leg " a = 7 / sqrt2 = 4.95#

#"From the above figure, sides are in the ratio ' a : a : asqrt2#

#"Given hypotenuse " = a sqrt2 = 7#

#:. a = 7 / sqrt2 = 7 / 1.4142 = 4.95#