This is an interesting problem (it was to me at least). It will involve some reasoning first before we get to the math.
What are we being asked here, really? Basically, this problem is saying that if we take the area under #y=4x-2x^2# and divide it by two, we should get the area under #y=mx# subtracted from the area under #y=4x-2x^2#.
Ok, that was kind of heavy. Let me demonstrate it with a picture.
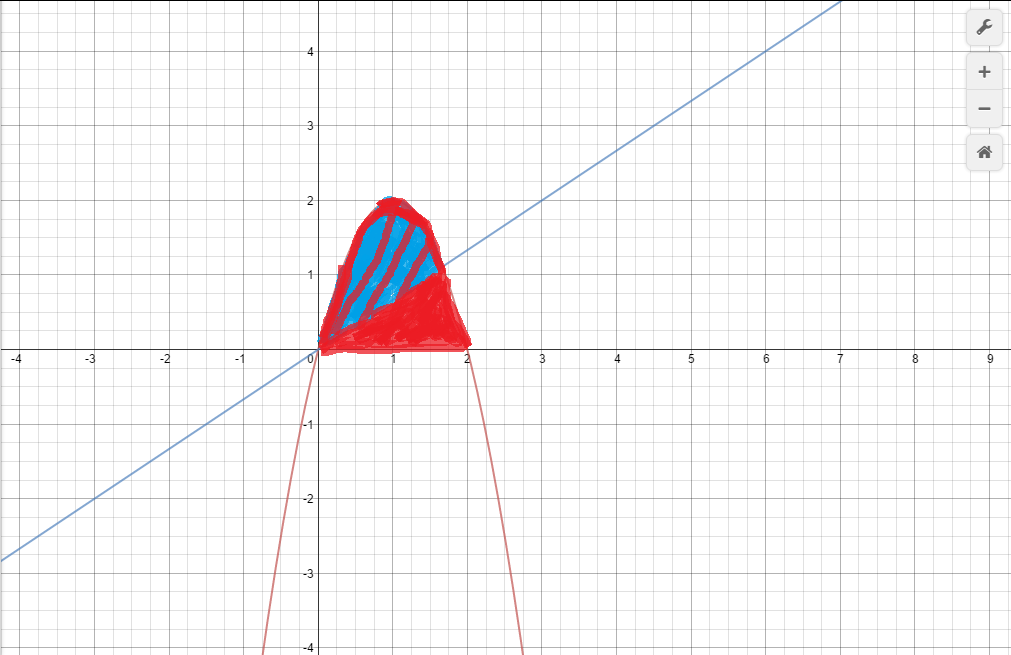
In this image, the red is the total area we care about under #y=4x-2x^2#, and blue is the area between #y=4x-2x^2# and the line #y=mx# (which is the line through the origin dividing the red region into two equal parts). If we take the blue area and subtract it from the red area, we should get half the red area - because the red area is split in half by the line.
The area of the red region is given by: #int_0^2 4x-2x^2dx#, while the area of the blue region is #int_0^2 4x-2x^2dx-int_0^2 mxdx# (remember, the area is split in half, so the blue region area is the red region area minus the area under #y=mx#). But wait! Because the area of the blue region is also the area of the red region divided by two (i.e. #(int_0^2 4x-2x^2dx)/2#), we can say:
#(int_0^2 4x-2x^2dx)/2=int_0^2 4x-2x^2dx-int_0^2 mxdx#
Using the sum rule, the problem becomes:
#(int_0^2 4x-2x^2dx)/2=int_0^2 4xdx-int_0^2 2x^2dx-int_0^2 mxdx#
Because #m# is a constant, we can pull it out:
#(int_0^2 4x-2x^2dx)/2=int_0^2 4xdx-int_0^2 2x^2dx-m int_0^2xdx#
We can then evaluate all of these integrals using the reverse power rule:
#(int_0^2 4x-2x^2dx)/2=4[x^2/2]_0^2-2[x^3/3]_0^2-m[x^2/2]_0^2#
#color(white)(XX)=4((2)^2/2-(0)^2/2)-2((2)^3/3-(0)^3/3)-m((2)^2/2-(0)^2/2)#
#color(white)(XX)=8-16/3-2m#
Our problem is now:
#(int_0^2 4x-2x^2dx)/2=8-16/3-2m#
Multiplying by 2:
#int_0^2 4x-2x^2dx=16-32/3-4m#
We have already evaluated #int_0^2 4x-2x^2dx#, and found it to be #8-16/3#:
#8-16/3=16-32/3-4m#
Now all that's left is to solve for #m#:
#8-16/3=16-32/3-4m#
#16/3=8-4m#
#16=24-12m->12m=8->m=8/12=2/3#
Thus the slope is #2/3#.



