A box with an initial speed of #2 m/s# is moving up a ramp. The ramp has a kinetic friction coefficient of #3/2 # and an incline of #(2 pi )/3 #. How far along the ramp will the box go?
2 Answers
Explanation:
We're asked to find how far the box will travel up the ramp, given its initial speed, the coefficient of kinetic friction, and the angle of inclination.
I will solve this problem using only Newton's laws and kinematics (i.e. without using work/energy).
NOTE: Ideally, the angle of inclination would be between
#0# and#pi/2# , so I'll choose the corresponding first-quadrant angle of#pi/3# .I will also take the positive
#x# -direction as *up the ramp.*
When the box reaches its maximum distance, the instantaneous velocity will be
#ul((v_x)^2 = (v_(0x))^2 + 2a_x(Deltax)#
where
-
#v_x# is the instantaneous velocity (which is#0# ) -
#v_(0x)# is the initial velocity -
#a_x# is the (constant) acceleration -
#Deltax# is the distance it travels (what we're trying to find)
Since the velocity
#0 = (v_(0x))^2 + 2a_x(Deltax)#
We also figure that the acceleration will be negative because it slows down and comes to a brief stop at its maximum height, so we then have
#0 = (v_(0x))^2 + 2(-a_x)(Deltax)#
And we can move it to the other side:
#ul(2a_x(Deltax) = (v_(0x))^2#
Rearranging for the distance traveled
#ulbar(|stackrel(" ")(" "Deltax = ((v_(0x))^2)/(2a_x)" ")|)#
We already know the initial velocity, so we need to find the acceleration of the box.
Let's use Newton's second law of motion to find the acceleration, which is
#ul(sumF_x = ma_x#
where
-
#sumF_x# is the net force acting on the box -
#m# is the mass of the box -
#a_x# is the acceleration of the box (what we're trying to find)
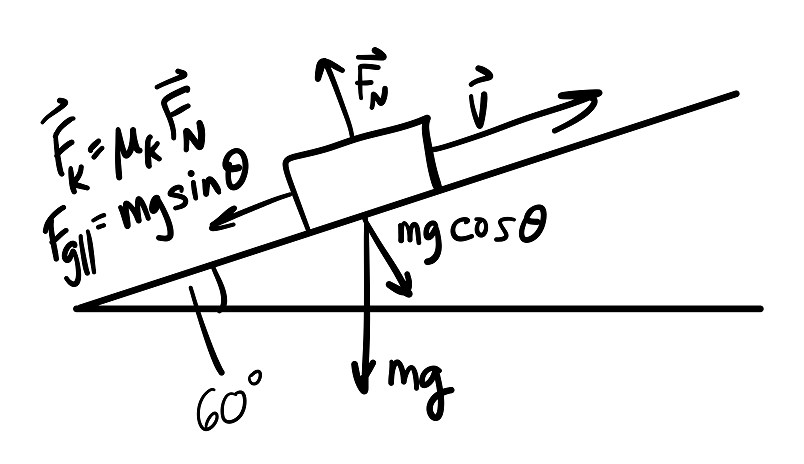
The only forces acting on the box are
-
the gravitational force (acting down the ramp), equal to
#mgsintheta# -
the friction force (acting down the ramp), equal to
#mu_kn#
And so we have our net force equation:
#sumF_x = mgsintheta + mu_kn# The normal force
#n# exerted by the incline is equal to
#n = color(purple)(mgcostheta)# So we can plug this in to the net force equation above:
#ul(sumF_x = mgsintheta + mu_kcolor(purple)(mgcostheta)#
Or
#ul(sumF_x = mg(sintheta + mu_kcostheta)#
Now, we can plug this in for
#sumF_x = ma_x#
#ma_x = mg(sintheta + mu_kcostheta)#
We can cancel the mass
#color(green)(ul(a_x = g(sintheta + mu_kcostheta)#
Now that we have found an expression for the acceleration, let's plug it into the equation
#Deltax = ((v_(0x))^2)/(2a_x)#
And we get
#color(red)(ulbar(|stackrel(" ")(" "Deltax = ((v_(0x))^2)/(2g(sintheta + mu_kcostheta))" ")|)#
We're given in the problem
-
#v_(0x) = 2# #"m/s"# -
#theta = (pi)/3# -
#mu_k = 3/2# -
and the gravitational acceleration
#g = 9.81# #"m/s"#
Plugging these in:
#color(blue)(Deltax) = ((2color(white)(l)"m/s")^2)/(2(9.81color(white)(l)"m/s"^2)(sin[(pi)/3] + 3/2cos[(pi)/3])) = color(blue)(ulbar(|stackrel(" ")(" "0.126color(white)(l)"m"" ")|)#
Here's my own attempt at this problem, using an alternative approach to Nathan's, to see if our answers agree. Like Nathan, I will assume that you mean to have the ramp right-side-up, i.e. an angle of
I also got
My approach here is via conservation of energy:
#DeltaE = DeltaK + DeltaU + W_(vecF_k) = 0# where:
- My coordinate axes are almost the usual vertical
#y# and horizontal#x# . Rightwards is#+x# , but downwards is#+y# .#DeltaK = 1/2 mv_f^2 - 1/2 mv_i^2 = m/2(v_f^2 - v_i^2)# #DeltaU = mvecgDeltavecy = mgy_f# , where#y_i = 0# ,#y_f < 0# , and#g > 0# . The potential energy becomes more negative due to the sign of#y_f# .#W_(vecF_k) = vecF_kd# is the counteracting work due to kinetic friction (negative w.r.t. the box, the system). In this case, I define
#d = sqrt((Deltax)^2 + (Deltay)^2) - 0 = sqrt(x_f^2 + y_f^2)# with#x_i = 0# and#x_f > 0# .#d# is then the final position,#< 0# .
Currently, we know we have a nonzero initial velocity and a zero final velocity when the box comes to a stop:
#=> DeltaK = -m/2v_i^2#
This so far gives:
#-m/2v_i^2 + mgy_f + vecF_kd = 0#
or
#m/2v_i^2 - mgy_f - vecF_kd = 0#
Using the sum of the forces:
#sum_i vecF_(_|_,i) = vecF_N - mvecgcostheta = 0#
So...
#0 = cancel(m)/2v_i^2 - cancel(m)gy_f - mu_kcancel(m)vecgcosthetad#
#=> 1/2 v_i^2 - gy_f - mu_kgcosthetad = 0#
Now, we can rewrite
#y_f = dsintheta < 0#
This gives:
#=> 1/2 v_i^2 - gdsintheta - mu_kgdcostheta = 0#
Solve for
#d = (1/2 v_i^2)/(gsintheta + mu_kgcostheta)#
#= (v_i^2)/(2g(sintheta + mu_kcostheta))# (which is also what Nathan found, by the way.)
So, in the end, we get:
#color(blue)(|d|) = (2^2)/(2(9.81)(sin(60^@) + 3/2cos(60^@)))#
#=# #color(blue)("0.126 m")#

