A box with an initial speed of #3 m/s# is moving up a ramp. The ramp has a kinetic friction coefficient of #3/4 # and an incline of #pi /8 #. How far along the ramp will the box go?
1 Answer
Explanation:
This question can be solved using a combination of kinematics and Newton's second law, or through the work-energy theorem. I will provide both solutions.
We have the following information:
#|->v_i=3"m"//"s"# #|->mu_k=3/4# #|->theta=pi/8# #|->g=9.81"m"//"s"^2#
Diagram:
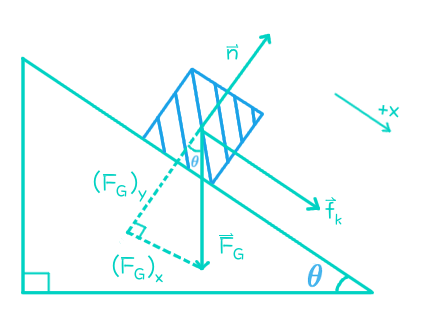
where
#vecn# is the normal force,#vecf_k# is the force of kinetic friction, and#vecF_G# is the force of gravity, decomposed into its parallel and perpendicular components
- I wil define up the ramp as the positive direction.
#color(darkblue)("Method 1: Newton's Second Law and Kinematics")# **
We can set up statements of the net force parallel (x) and perpendicular (y).
#color(darkblue)(F_(x"net")=sumF_x=-f_k-(F_G)_x=ma_x)#
#color(darkblue)(F_(y"net")=sumF_y=n-(F_G)_y=0)# Note no acceleration in the vertical direction (dynamic equilibrium).
Therefore, we have
The force of kinetic friction is given by
#color(darkblue)(f_k=mu_kn)#
We can find the perpendicular component of gravity and consequently the magnitude of the normal force using trigonometry. We can see from the above diagram that the angle between the force of gravity and the vertical is the same as the angle of incline of the ramp.
#cos(theta)="adjacent"/"hypotenuse"#
#=>cos(theta)=(F_G)_y/(F_G)#
#=>color(darkblue)((F_G)_y=F_Gcos(theta))#
Similarly, we find that
As
#color(darkblue)(n=mgcos(theta))#
Therefore:
#color(darkblue)(f_k=mu_k*mgcos(theta))#
Substituting this and the equation we derived for the force of gravity parallel above into our statement for the net force parallel:
#-mu_kcancelcolor(skyblue)(m)gcos(theta)-cancelcolor(skyblue)(m)gsin(theta)=cancelcolor(skyblue)(m)a_x#
#=>color(blue)(a_x=-g(mu_kcos(theta)+sin(theta)))#
We can now use this kinematic equation to find the distance traveled up the ramp:
#v_f^2=v_i^2+2aDeltas#
Solving for
#Deltas=(cancel(v_f^2)-v_i^2)/(2a)#
Substituting in the equation we derived above for the acceleration:
#color(blue)(Deltas=(-v_i^2)/(-2g(mu_kcos(theta)+sin(theta)))#
Now we can substitute in our known values:
#Deltas=(3"m"//"s")^2/(2(9.81"m"//"s"^2)(3/4cos(pi/8)+sin(pi/8))#
#=>color(blue)(~~0.42"m")#

