Question

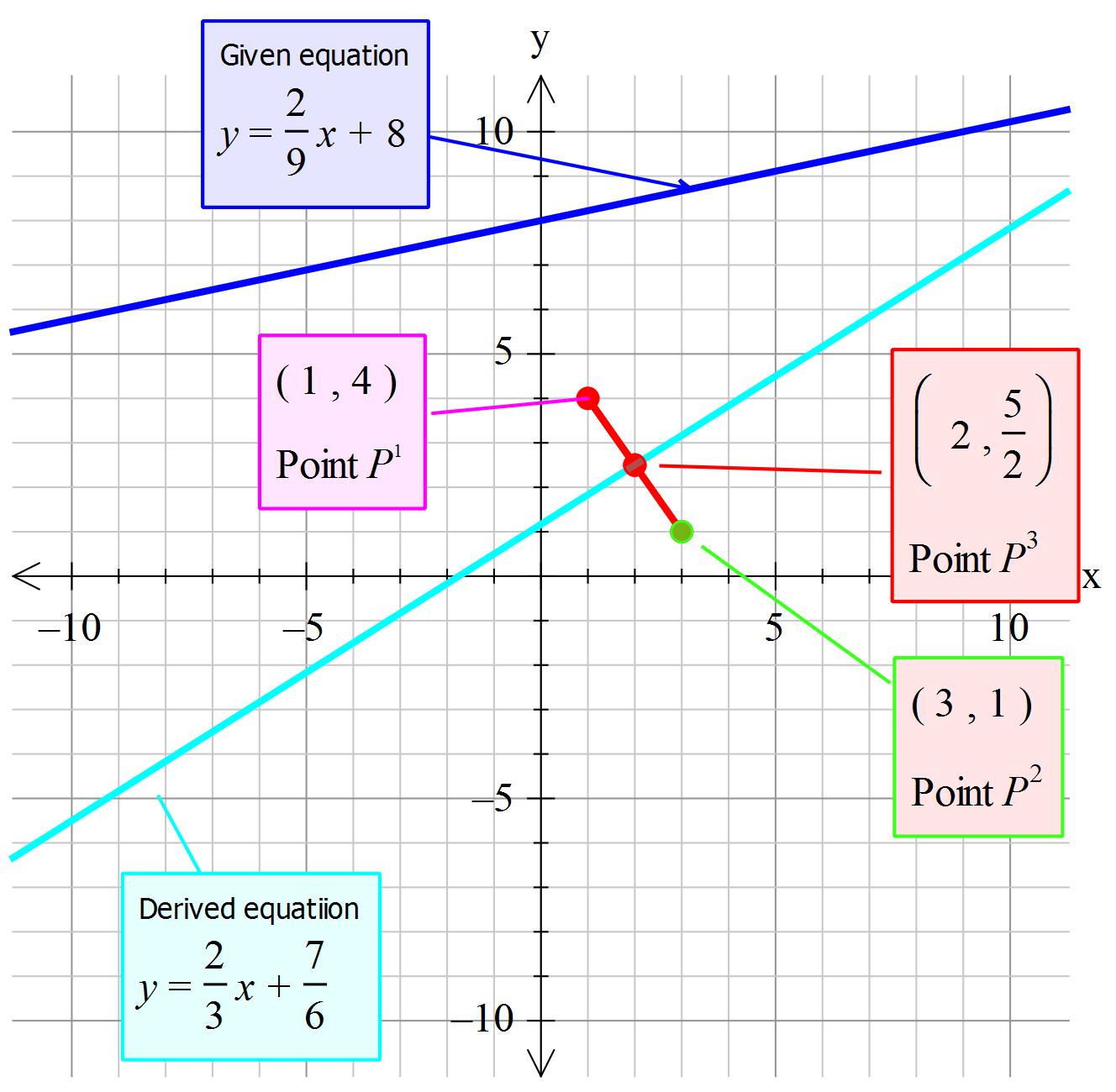
A circle has a center that falls on the line `y = 2/9x +8` and passes through `( 3 ,1 )` and `(1 ,4 )`. What is the equation of the circle?

Answer 1

`color(blue)((x-123/8)^2+(y-137/12)^2 = r^2)`

Explanation:

Standard equation of a circle: `(x-a)^2+(y-b)^2=r^2`
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let point `P_1->(x_1,y_1)->(1,4)`
Let point `P_2->(x_2,y_2)->(3,1)`
Let point `P_3->(x_3,y_3)->(?,?)`
Let the gradient `P_1" to "P_2 ->m`

'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`color(blue)("Method")`

Determine gradient of line between the two given points. The line normal (perpendicular) to it will pass through the centre of these points and have the negated inverse of their gradient.

Calculate the equation of this line. Where it crosses `y=2/9x+8` will be the centre of the circle.
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`color(blue)("Determine centre point " P_3 " & gradient between "P_1 "&"P_2 )`

Centre point is the mean value
`color(blue)(P_3->(x_3,y_3)->( (3+1)/2,(1+4)/2) =(2,5/2))`

`color(blue)(m=(y_2-y_1)/(x_2-x_1) = (1-4)/(3-1) = -3/2)`

'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

`color(blue)("Determine the equation of the second line")`

known: `"gradient "-> -1/m = +2/3`

passes through point `P_3=(2,5/2)`

Thus `y=mx+c` becomes:

`" "5/2=2/3(2)+c -> 5/2=4/3+c`

`" "=> c= 7/6`

So equation of second line is:

`color(blue)(" "y=2/3x+7/6)`

'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`color(blue)("Determine the centre of the circle")`

This occurs where the two lines cross.

Equate then to each other through `y` giving

`" "2/9x+8" " =" " y" " =" " 2/3x+7/6`

`" "2/3 x-2/9 x=8-7/6`

`" "4/9x=41/6`

`color(blue)(" "x=123/8)`
'.........................................................

Substitute for `x` in `y=2/3x+7/6`

`y=2/3(123/8)+7/6`

`color(blue)(y=137/12)`

`color(blue)("Circle centre at "(x,y)->(123/8,137/12)`
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

`color(blue)("Equation of the circle")`

`color(blue)((x-123/8)^2+(y-137/12)^2 = r^2)`