Question

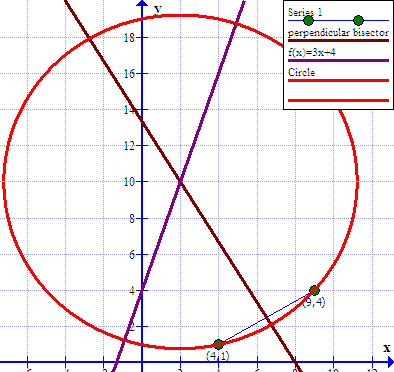
A circle has a center that falls on the line `y = 3x +4` and passes through `(4 ,1 )` and `(9 ,4 )`. What is the equation of the circle?

Answer 1

`(x-2)^2+(y-10)^2=85`

Explanation:

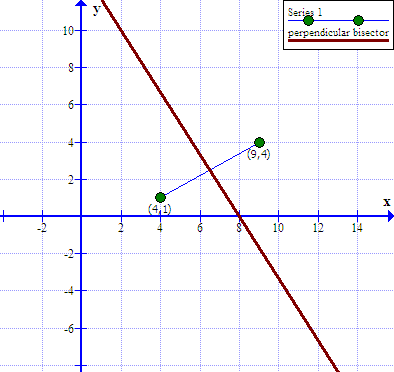
Part 1: Find the right bisector of the line segment between `color(black)(""(4,1))` and `color(black)(""(9,4))`

The line segment between `(4,1)` and `(9,4)` has a midpoint at
`color(white)("XXX")((4+9)/2,(1+4)/2)=(13/2,5/2)`
The slope of this line segment is
`color(white)("XXX")(Deltay)/(Deltax)=(4-1)/(9-4)=3/5`
`rarr` the slope of its perpendicular bisector is `(-5/3)`

Using the slope-point form, the equation of the perpendicular bisector is
`color(white)("XXX")y-5/2=(-5/3)(x-13/2)`
`color(white)("XXX")6y-15=-10x+65`
`color(white)("XXX")y=(-10x+80)/6=(-5x+40)/3`

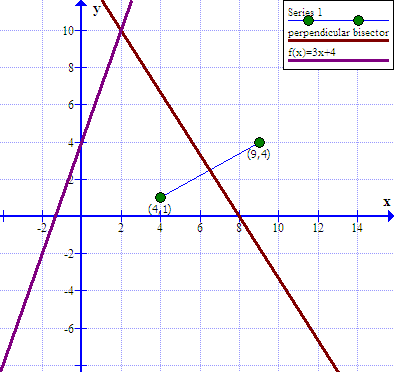
Part 2: find the center of the circle

Since the center of the circle is equal distance from all points on its circumference.
the center of the circle must be on the perpendicular bisector
(which as we have seen has the equation `color(brown)(y=(-5x+40)/3`

We have also been told that the center is on the line `color(purple)(y=3x-4)`

Solving the system of linear equations
`color(white)("XXX"){(color(brown)(y=(-5x+40)/3)),(color(purple)(y=3x-4)):}`
Gives the center of the circle at `color(red)((x_c,y_c)=(2,10))`

Part 3: Calculate the radius of the circle

The radius of the circle is the distance from the center to any point on the circumference.

Using `(""(4,1))` as a point on the circumference, we have
`color(white)("XXX")color(blue)(r)=sqrt(2-4)^2+(10-1)^2)color(blue)(=sqrt(85))`

Part 4: Insert the calculated values into the standard formula for a circle

The standard formula for a circle with center `color(red)(""(x_c,y_c))` and radius `color(blue)(r)` is
`color(white)("XXX")(x-color(red)(x_c))^2+(y-color(red)(y_c))^2=color(blue)(r)^2`

Using the values determined above
`color(white)("XXX")(x-2)^2+(y-10)^2=85`