A circle has a chord that goes from #( 3 pi)/4 # to #(5 pi) / 4 # radians on the circle. If the area of the circle is #81 pi #, what is the length of the chord?

1 Answer
Bisma J.
Dec 24, 2017

Obtain the radius #r = 9# from the area, visualize the problem if needed, and find that the chord must be double the sine of the angle inside the triangle times the radius, to get #L_"chord" = 9 sqrt(2)#.

Explanation:

First, let's obtain the radius from the area:

#A = pi r^2 = 81 pi#

Here, #pi# cancels out:

#r^2 = 81#

And taking the square root gets us:

#r = 9#.

Here's what the circle looks like:

enter image source here

Just like any other circle. Let's just say its radius is #9#.

Anyway, we now need a chord from #(3 pi)/4# to #(5 pi)/4#.

#pi# itself is halfway around the circle. Since we're taking quarters of halfs of the circle, let's split it into eighths:

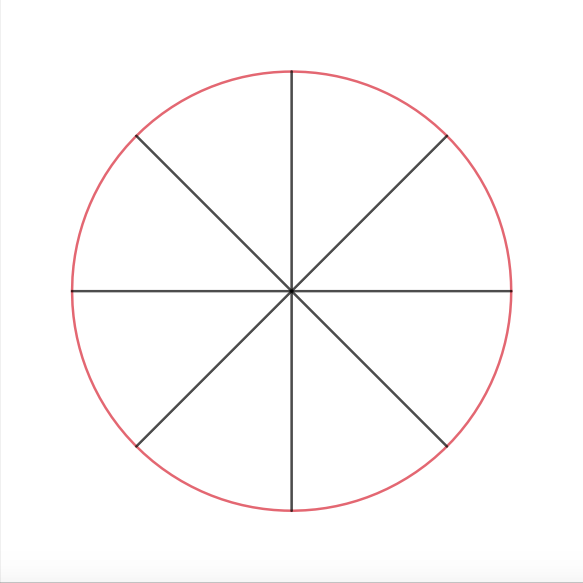
enter image source here

Let's start rotating! We know to start at the rightmost point of the circle, which is in this case #(9, 0)#:

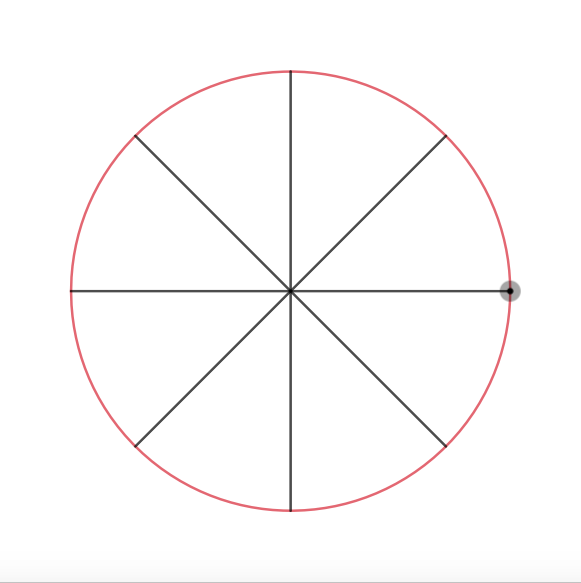
enter image source here

Then we can start rotating it by #(3 pi)/4#, which is #3# quarters of half of the circle, or equivalently, #3# eigths of the circle:

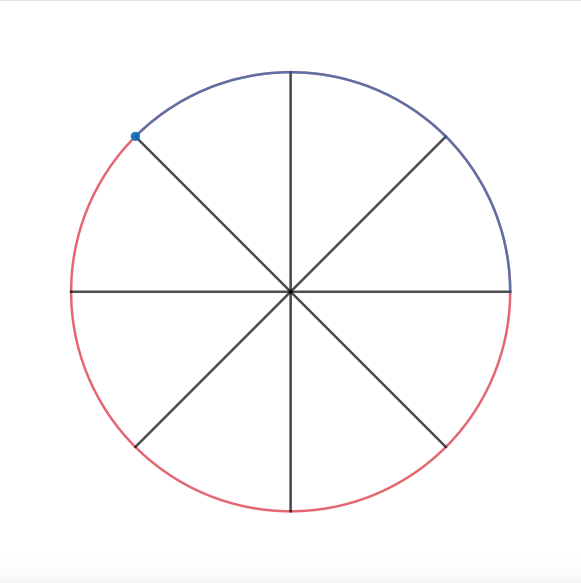
enter image source here

How much left do we need to go?

#(5 pi)/4 - (3 pi)/4 = (2 pi)/4 = pi/2#

Ah, half-#pi# radians left! That's half of a half of the circle, or, a quarter of the circle, which is #2# eights:

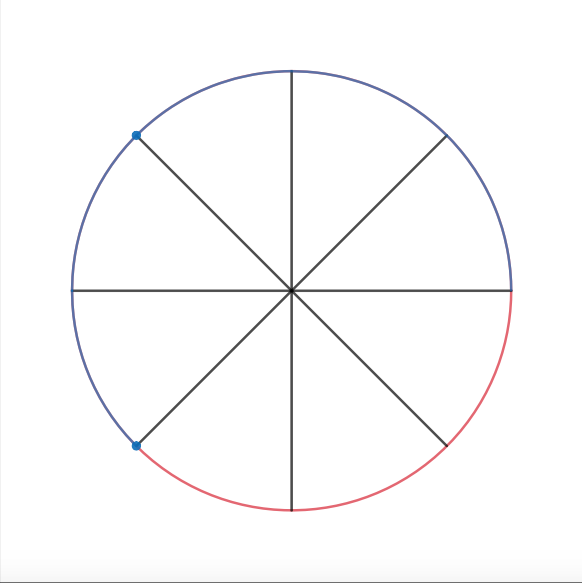
enter image source here

We could now draw the chord between these two points, and lift off slices we no longer need:

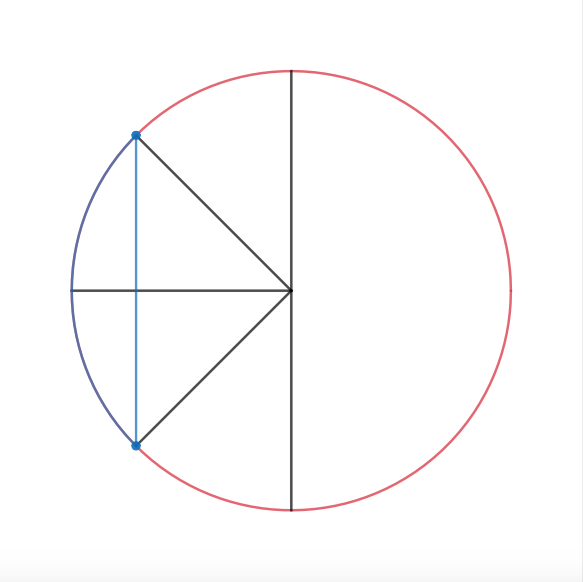
enter image source here

Those familiar with the unit circle might immediately get that the length of the chord must be double the sine of the angle inside that triangle, times the radius.

Why? The sine is defined as the ratio of the side of the triangle opposite of the angle, to the hypotenuse:

#sin(theta) = "Opposite"/"Hypotenuse"#

Multiplying by the hypotenuse, which is in this case the radius, #r = 9#, should get us the length of the opposite side:

#r * sin(theta) = r * "Opposite"/r = "Opposite"#

But, what is the angle inside the triangle?

Well, we could immediately see that it is a quarter of the semicircle, which is #pi/4# radians.

The length of the side opposite to that angle would be

#L_"opposite" = r * sin(pi/4) = 9 * (sqrt(2))/2 = (9 sqrt(2))/2#

And the chord is double that length:

#L_"chord" = 2 * L_"opposite" = 2 * (9 sqrt(2))/2 = 9 sqrt(2)#

Related questions
See all questions in Circle Arcs and Sectors
Impact of this question
2228 views around the world
You can reuse this answer
Creative Commons License