Question

A circular arc of length 16 ft subtends a central angle of 25°. How do you find the radius of the circle?

Answer 1

Consider the following diagram

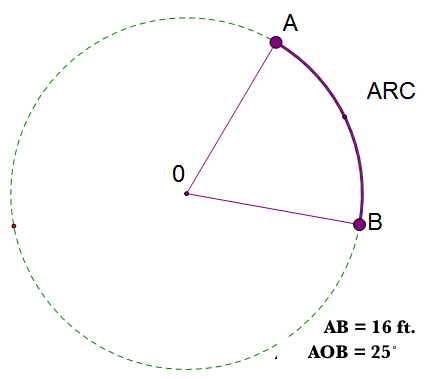
The formula for arc length is `s = theta xx r`, where `r` is the radius, `theta` is the center angle in radians and `s` is the arc.

We can convert `25˚` to radians using the conversion factor `pi/180`.

`theta" in radians" = 25 xx pi/180 = (5pi)/36`

Now, solving for `r` in the formula we have `s/theta = r`

`16/((5pi)/36) = r`

`(36 xx 16)/(5pi) = r`

`36.67 = r`

The radius measures 36.67 feet.

Hopefully this helps!