A cube and a regular octahedron are carved out of of unit-radius wooden spheres . If the vertices are on the spheres, how do you prove that their volumes compare with that of the sphere, in the proportions #3/sqrt 2 : 2 : pi?#
1 Answer
The proportion is
Explanation:
Volume of a sphere of radius
Now let us consider a cube carved in unit sphere. It should appear as follows:
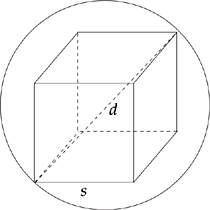
As the diameter of sphere is the longest diagonal of sphere, which is
A regular octahedron is a solid object made of eight equilateral triangles and appears as shown below. It is made of two tetrahedrons and volume of an octahedron of side
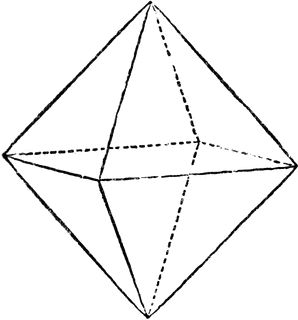
Let us consider an octahedron in a sphere, so that when a sphere is divided into eight equal parts each part contains an equilateral triangle. Using Pythagoras theorem, the side of a tetrahedron will be given by
Hence, volume of tetrahedron in a sphere of unit radius will be
Now we have to find ratio of volume of such cube, octahedron and sphere and it is
and multiplying each term by
or
