Question

A cylindrical pillar, with a regular nonagonal cross-section, has to be carved out of a right circular cylindrical sandal wood. If the height is 10' and diameter of the base is 1', how do you prove that the minimum possible scrap is 0.623 cft, nearly?

Answer 1

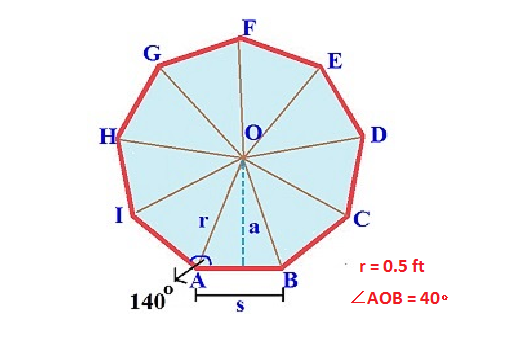
The nonagonal cross section of the pillar has been shown in the above figure. Here `r` represents the radius of the original cylindrical pillar. So `r= 1/2ft ("given")`

So area of the nonagonal cross section is equal to the total area of 9 identical isosceles triangles each having area equal to the area of `DeltaABO`

So the nonagonal cross sectional area

`A=9xxDeltaABO=9xx1/2r^2xxsin/_AOB`

`=9/2xx(1/2)^2xxsin40^@=9/8xxsin40^@sqft`

Height of the pillar `h=10ft`

So volume of the pillar of nonagonal cross section

`V_2=Ah=90/8xxsin40^@cuft`

The original volume of the cylindrical pillar
`V_1=pir^2h=pi(1/2)^2xx10cuft`

So the volume of the minimum possible scrap is

`V_"scrap"=V_1-V_2`

`=pi(1/2)^2xx10cuft-90/8xxsin40^@cuft~~0.623cft`